120.三角形最小路径和

题目

• 给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

例题

• [

• [ 2 ],

• [3 , 4 ],

• [6 , 5 , 7 ],

• [ 4 , 1 ,8 , 3 ]

• ]

自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

解题

• 动态规划：从上或者从下依次往上遍历，直到走到终点，比较最短的路程。

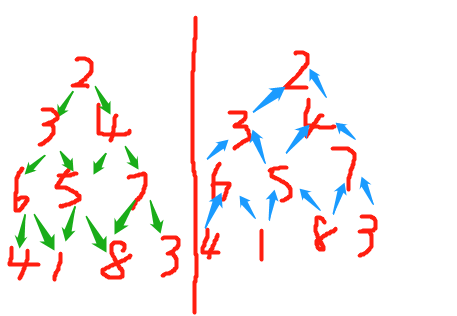
• 可以发现：从上—除了两侧的只有一条路来 / 从下—都是有两条路来

• 从上到下

第一个：res[i][0] = res[i-1][0] + triangle[i][0];
中间的：res[i][j] = triangle[i][j] + min(res[i-1][j-1],res[i-1][j]);
最后个：res[i][i]  = res[i-1][i-1] + triangle[i][i];

• 从下到上

triangle[i][j] += min(triangle[i+1][j],triangle[i+1][j+1]);

---

代码

int minimumTotal(vector<vector<int>>& triangle) {

	int lenX = triangle.size();
	vector<vector<int>>res(lenX, vector<int>(lenX, 0));
	res[0][0] = triangle[0][0];
	for (int i = 1; i < lenX; i++) {
		//第一个数据
		int temp = i;
		res[i][0] = res[i - 1][0] + triangle[i][0];
		//中间数据
		for (int j = 1; j < temp; j++) {
			res[i][j] = triangle[i][j] + min(res[i - 1][j - 1], res[i - 1][j]);
		}
		//最后一个数据
		res[i][temp] = res[i - 1][temp - 1] + triangle[i][temp];
	}
	sort(res.back().begin(), res.back().end());
	return res.back()[0];
}

---

int minimumTotal(vector<vector<int>>& triangle) {
	int n = triangle.size();

	for (int i = n - 2; i >= 0; i--) {
		for (int j = 0; j <= i; j++) {
			triangle[i][j] += min(triangle[i + 1][j], triangle[i + 1][j + 1]);
		}
	}
	return triangle[0][0];
}