785. 判断二分图

题目

• 给定一个无向图graph，当这个图为二分图时返回true。

• 如果我们能将一个图的节点集合分割成两个独立的子集A和B，并使图中的每一条边的两个节点一个来自A集合，一个来自B集合，我们就将这个图称为二分图。

• graph将会以邻接表方式给出，graph[i]表示图中与节点i相连的所有节点。每个节点都是一个在0到graph.length-1之间的整数。这图中没有自环和平行边： graph[i] 中不存在i，并且graph[i]中没有重复的值。

---

理解：graph[i]代表i结点所相连接的所有节点

二分图理解：

• 二分图：顶点由两个集合A和集合B组成，且所有边的两个顶点正好分别处于两个集合里
• 更形象化地去表示：我们可以用两种颜色代表这两个集合，相邻的顶点不能是同一种颜色
• 下图右边例子：
  1. 对顶点0来说，1、2、3和它相邻所以不同色，
  2. 对顶点1，2来说，1和2因此同色，不是二分图

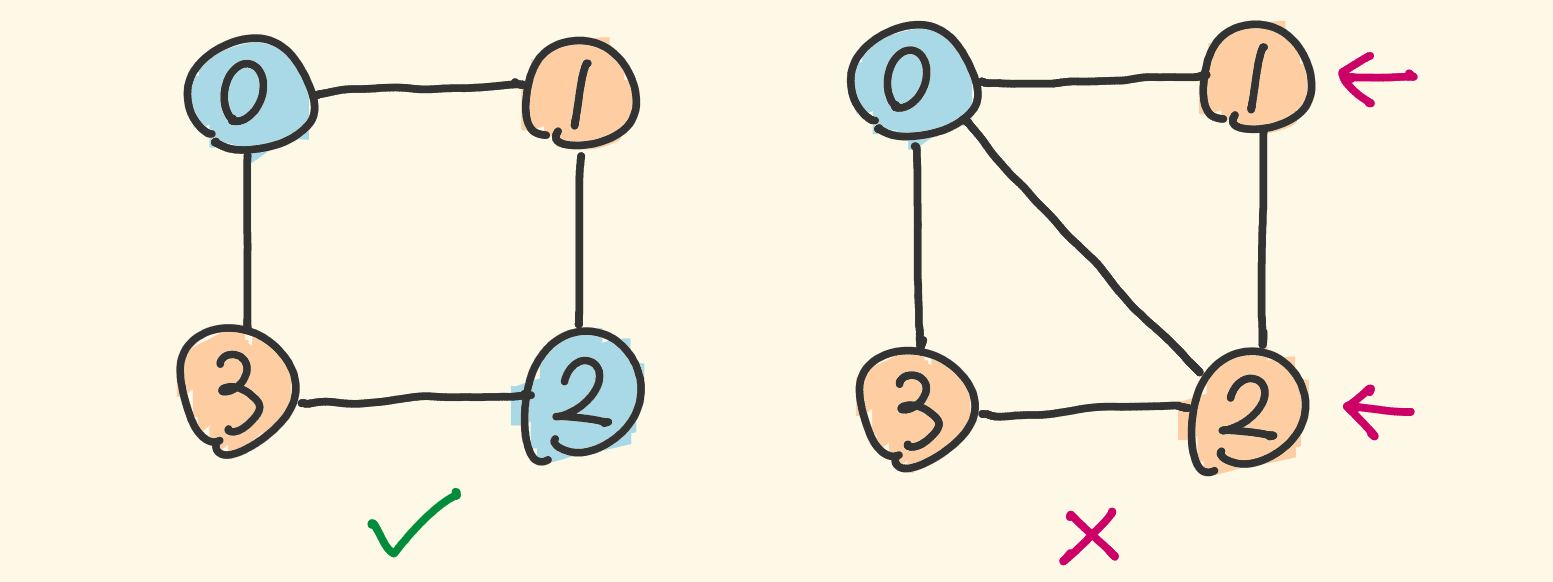
总结：将点到点的集合——划分为不相交的两个子集（点在两个子集和里），同时所对应的两个 顶点i 和 顶点j 分别在不同的集合中。

例题

解题

• 动态规划：题解如上，分个数讨论，依次从1、2、3、4往上，在前者的基础上讨论现在的可能情况

---

代码

//-1——未染色
// 0——染为0
// 1——染为1
vector<int> v;
bool isBipartite(vector<vector<int>>& graph) {
	int n = graph.size();

	vector<int> v(n, -1);        // 给所有节点标记为 -1（未染色）
	for (int i = 0; i < n; i++) { // 依次遍历每一个节点
		if (v[i] == -1) { // 未染色入栈进行操作
			queue<int> q;
			q.push(i);
			v[i] = 0;   //将其染为0
			while (!q.empty())
			{
				int cur = q.front();                //当前节点颜色
				int cur_neighbor = (v[cur] == 0 ? 1 : 0);// 记录接下来相邻节点要染的另一种颜色    
				q.pop();

				for (int node_neighbor : graph[cur]) // 遍历节点node的相邻节点
				{
					if (v[node_neighbor] == -1)   //没染色，进行染色，同时入栈
					{
						q.push(node_neighbor);
						v[node_neighbor] = cur_neighbor;
					}
					else if (v[node_neighbor] != cur_neighbor) //染色了，若颜色相同，说明在同一个子集里
					// 相邻节点染色 不是 cur_neighbor
						return false;
				}
			}

		}
	}
	return true;
}