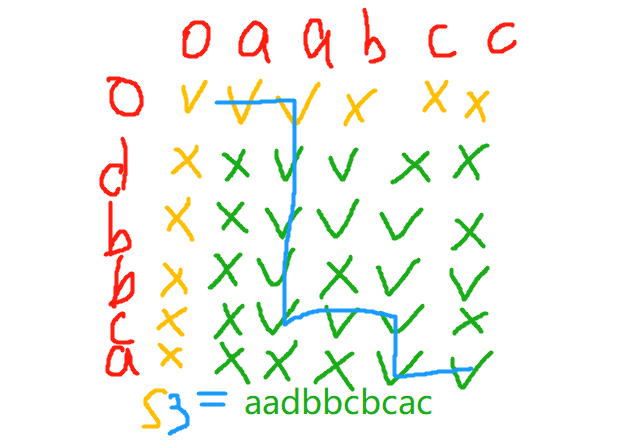97. 交错字符串
题目
- 给定三个字符串 s1, s2, s3, 验证 s3 是否是由 s1 和 s2 交错组成的。
例题
输入: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
输出: true
输入: s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbbaccc”
输出: false
理解:字符串问题用动态规划,逐步思考和上一个字符串的关系
字符串画表,进行路径规划
dp[i][j] = dp[i-1][j]&&s1[i-1]==s3[i+j-1] || dp[i][j-1]&&s2[j-1]==s3[i+j-1];
画表画表
解题
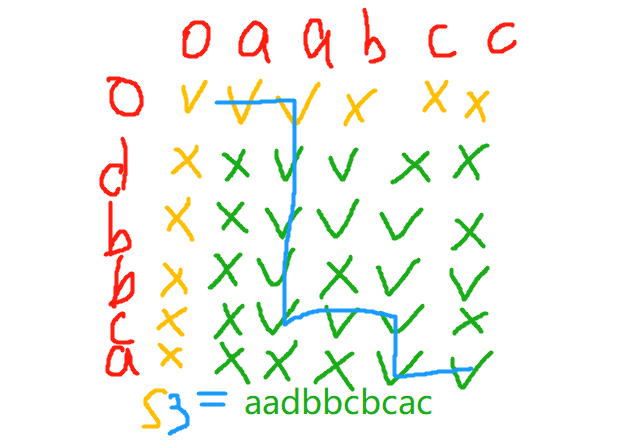
- 初始化列表
- 路径规划——两条路径,前提条件的保证和选择
- dp[i][j] =
dp[i-1][j]&&s1[i-1]==s3[i+j-1] || dp[i][j-1]&&s2[j-1]==s3[i+j-1]
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| bool isInterleave(string s1, string s2, string s3) {
if (s1.size() + s2.size() != s3.size())
return false;
int n = s1.size();
int m = s2.size();
vector<vector<bool>>dp(n + 1, vector<bool>(m + 1, false));
dp[0][0] = true;
for (int i = 1; i < n + 1; i++) {
dp[i][0] = dp[i - 1][0] && s1[i - 1] == s3[i - 1];
}
for (int i = 1; i < m + 1; i++) {
dp[0][i] = dp[0][i - 1] && s2[i - 1] == s3[i - 1];
}
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < m + 1; j++) {
dp[i][j] = dp[i - 1][j] && s1[i - 1] == s3[i + j - 1] ||
dp[i][j - 1] && s2[j - 1] == s3[i + j - 1];
}
}
return dp[n][m];
}
|
类似题目
416. 分割等和子集
题目
- 给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
例题
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].
输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.
理解:让集合元素相加 target = sum / 2
动态规划:对于依次使用集合中元素,考虑所有能组合成的可能性
dp[ i ][ j ] = dp[ i-1 ][ j ] || nums[ i ]==j || dp[ i-1 ][ j - nums[i]]
1.上可以,下不加也一定可以
2.当num[i] =j时也一定可以
3.当 j>nums[i]时,dp[i-1][j-nums[i]]也为真时,其也为真
画表画表
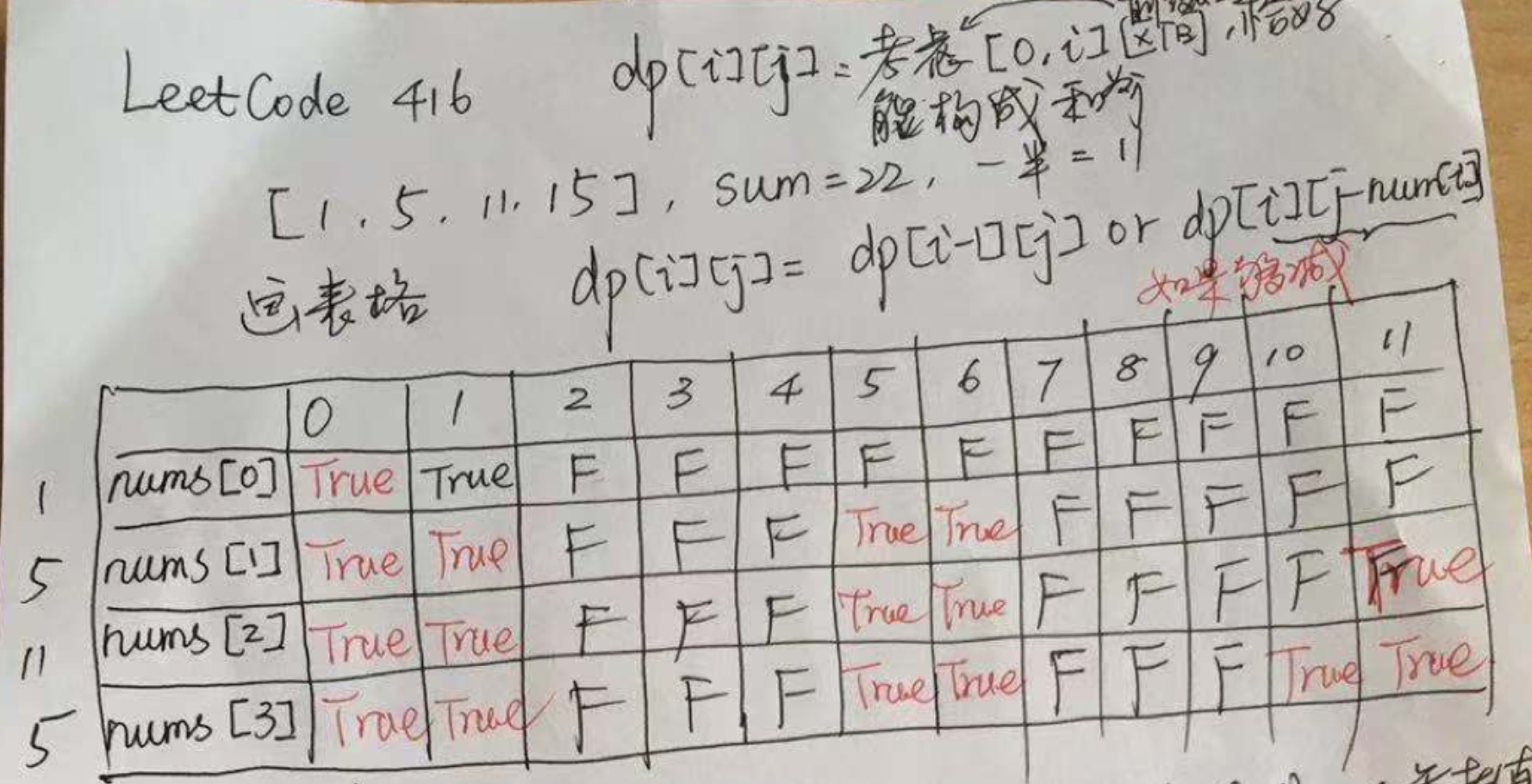
- 初始化列表
- 路径规划——三种可能,前提条件的保证和选择
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| bool canPartition(vector<int>& nums) {
int n = nums.size();
if (n <= 1)return false;
int sum = 0;
for (auto it : nums) {
sum += it;
}
if (sum % 2 == 1)return false;
int target = sum / 2;
vector<vector<bool>>dp(n, vector<bool>(target + 1, 0));
dp[0][0] = true;
if (nums[0] <= target) {
dp[0][nums[0]] = true;
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < target + 1; j++) {
dp[i][j] = dp[i - 1][j];
if (nums[i] <= j) {
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
}
}
if (dp[i][target]) {
return true;
}
}
return dp[n - 1][target];
}
|
72. 编辑距离
题目:给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
- 你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
例题

解题
三种移动方法:1.删除 2. 替换 3.插入
删除和替换和插入操作数是一样的为1,但是当插入的新字符 = 对应字符,操作数为0
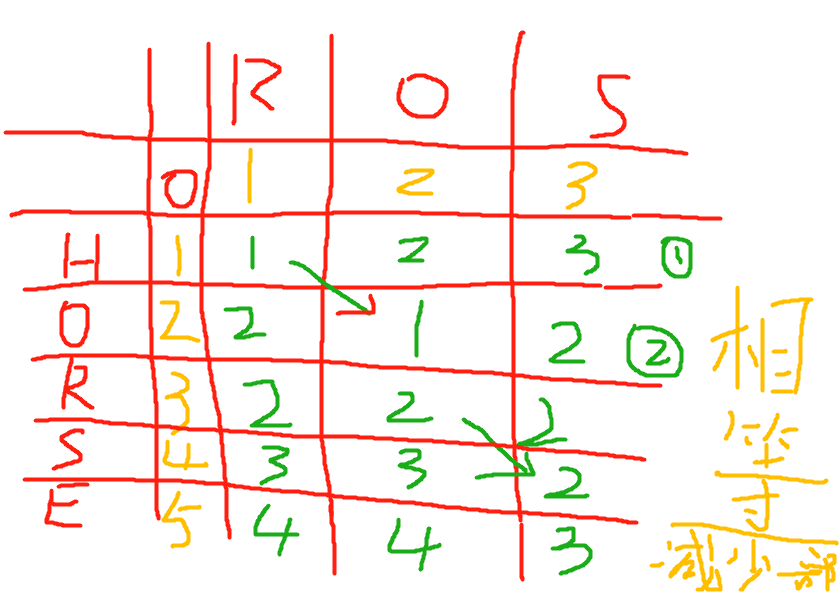
1.初始化 dp[i][0] = i;
2.
int temp1 = dp[i-1][j] + 1;
int temp2 = dp[i][j-1] + 1;
int temp3 = dp[i-1][j-1];
if(word1[i-1]!= word2[j-1])temp3++;
- dp[i][j] = min(temp1,min(temp2,temp3));
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| int minDistance(string word1, string word2) {
int len1 = word1.size();
int len2 = word2.size();
if (len1*len2 == 0)return max(len1, len2);
vector<vector<int>>dp(len1 + 1, vector<int>(len2 + 1));
for (int i = 0; i < len1 + 1; i++) {
dp[i][0] = i;
}
for (int i = 0; i < len2 + 1; i++) {
dp[0][i] = i;
}
for (int i = 1; i < len1 + 1; i++) {
for (int j = 1; j < len2 + 1; j++) {
int temp1 = dp[i - 1][j] + 1;
int temp2 = dp[i][j - 1] + 1;
int temp3 = dp[i - 1][j - 1];
if (word1[i - 1] != word2[j - 1])
temp3++;
dp[i][j] = min(temp1, min(temp2, temp3));
}
}
return dp[len1][len2];
}
|
1143. 最长公共子串
题目
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
例如,”ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
- 输入:text1 = “abcde”, text2 = “ace”
- 输出:3
- 解释:最长公共子序列是 “ace”,它的长度为 3。
- 输入:text1 = “abc”, text2 = “def”
- 输出:0
- 解释:两个字符串没有公共子序列,返回 0。
- 初始化dp [0][ i ] = 0 dp [ j ][0] = 0
- dp方程
if(text1[ i-1 ]=text2[ j-1])
dp[ i ][ j ] = dp[i-1 ][ j-1 ] +1;
else
dp[ i ][ j ] = max(dp[i-1 ][ j ],dp[i ][ j-1 ];)

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| int longestCommonSubsequence(string text1, string text2) {
int m = text1.size();
int n = text2.size();
vector<vector<int>>dp(m + 1, vector<int>(n + 1, 0));
for (int i = 1; i < m + 1; i++) {
for (int j = 1; j < n + 1; j++) {
if (text1[i - 1] == text2[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1;
else
dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
}
}
return dp[m][n];
}
|
718.最长重复子数组
题目:
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
例题:
- 输入:
- A: [1,2,3,2,1]
- B: [3,2,1,4,7]
- 输出:3
- 解释:
- 长度最长的公共子数组是 [3, 2, 1] 。