Zichuan365' Blog HomeArchivesCategoriesGalleryAbout
剑指Offer68 / # 48 - 68
|剑指Offer48 - 68

48 - 68

48. 最长不含重复字符的子字符串

  • 请从字符串中找出一个最长的不包含重复字符的子字符串，计算该最长子字符串的长度。

  • 输出
  • 输入: “abcabcbb”
  • 输出: 3
  • 解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
  • 输入: “bbbbb”
  • 输出: 1
  • 解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
  • 输入: “pwwkew”
  • 输出: 3
  • 解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
  • 请注意，你的答案必须是 子串 的长度，”pwke” 是一个子序列，不是子串。

  • 方法：双指针 + 辅助数组，最多256个字符

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int lengthOfLongestSubstring(string s) {
	if (s.size() <= 1)
		return s.size();

	vector<int>arr(256, 0);
	int left = 0;
	int right = 0;
	int res = 0;

	while (right < s.size()) {
		char tempChar = s[right++];//右是开，区间外第一个字符
		arr[tempChar]++;

		while (arr[tempChar] > 1) {  //说明有重复的
			arr[s[left]]--;//左边字符去除
			left++;//左值针移动
		}
		res = max(res, right - left);
	}
	return res;
}

49.丑数

  • 我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

  • 输出

  • 输入: n = 10

  • 输出: 12

  • 解释: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。

  • 方法：丑数本身是丑数，丑数是在丑数的基础上*2 或 *3 或 *5

  • 所以我们在三个丑数数组中选取最小的数来组成，三个变量a、b、c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int nthUglyNumber(int n) {
	int a = 0, b = 0, c = 0;
	vector<int>dp(n, 0);
	dp[0] = 1;
	//在三个顺序数组中拿出最小的数组成
	for (int i = 1; i < n; i++) {
		int temp1 = dp[a] * 2;
		int temp2 = dp[b] * 3;
		int temp3 = dp[c] * 5;

		dp[i] = min(temp1, min(temp2, temp3));
		if (dp[i] == temp1)a++;
		if (dp[i] == temp2)b++;
		if (dp[i] == temp3)c++;
	}
	return dp[n - 1];
}

50.第一个只出现一次的字符

  • 在字符串 s 中找出第一个只出现一次的字符。如果没有，返回一个单空格。 s 只包含小写字母。

  • 输出

  • s = “abaccdeff”

  • 返回 “b”

  • s = “”

  • 返回 “ “

  • 方法：哈希表统计

1
2
3
4
5
6
7
8
char firstUniqChar(string s) {
	unordered_map<char, int> t;
	for (auto temp : s) t[temp]++;

	for (char temp : s)
		if (t[temp] == 1) return temp;
	return ' ';
}

51.数组中的逆序对

  • 方法：归并

  • 在归并排序的基础上，加上两行。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
int res = 0;
void merge(vector<int>&arr, vector<int>&temp, int L, int mid, int R) {
	int p1 = L;
	int p2 = mid + 1;
	int p = L;
	while (p1 <= mid && p2 <= R) {
		if (arr[p1] <= arr[p2]) {
			temp[p++] = arr[p1++];
			res += p2 - (mid + 1);
		}
		else
			temp[p++] = arr[p2++];
	}
	while (p1 <= mid) {
		temp[p++] = arr[p1++];
		res += p2 - (mid + 1);
	}
	while (p2 <= R)  temp[p++] = arr[p2++];

	copy(temp.begin() + L, temp.begin() + R + 1, arr.begin() + L);
}

void sort(vector<int>&arr, vector<int>&tmp, int L, int R) {
	if (L >= R)
		return;

	int mid = (L + R) / 2;
	sort(arr, tmp, L, mid);
	sort(arr, tmp, mid + 1, R);

	merge(arr, tmp, L, mid, R);
}

int reversePairs(vector<int>& nums) {
	vector<int>tmp(nums.size());
	sort(nums, tmp, 0, nums.size() - 1);

	return res;
}

52.两个链表的第一个公共节点

  • 输入两个链表，找出它们的第一个公共节点。

  • 输出
    img1

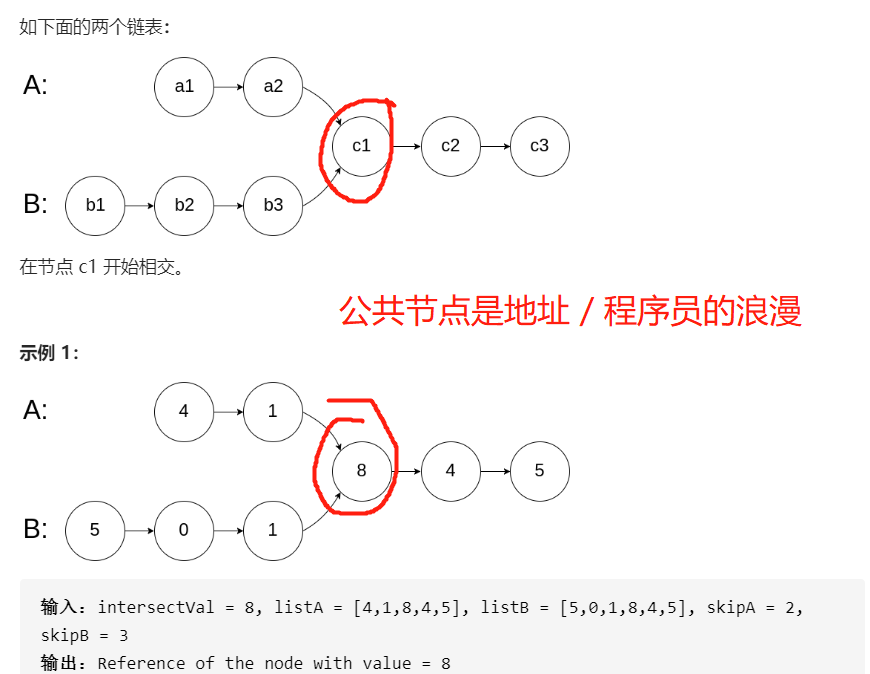
  • 方法：

  • a + c + b = b + c + a程序员的浪漫

  • 太浪漫了 两个结点不断的去对方的轨迹中寻找对方的身影

1
2
3
4
5
6
7
8
9
10
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
	ListNode *h1 = headA, *h2 = headB;

	while (h1 != h2) {
		h1 = h1 == NULL ? headB : h1->next;
		h2 = h2 == NULL ? headA : h2->next;
	}
	return h1;

}

53-1.在排序数组中查找数字出现次数

  • 统计一个数字在排序数组中出现的次数。

  • 输出

  • 输入: nums = [5,7,7,8,8,10], target = 8

  • 输出: 2

  • 输入: nums = [5,7,7,8,8,10], target = 6

  • 输出: 0

  • 方法：二分法！！有序一般都是二分法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int search(vector<int>& nums, int target) {
	int left = 0;
	int right = nums.size() - 1;
	int res = 0;
	while (left < right) {
		int mid = left + right >> 1;
		if (nums[mid] < target)
			left = mid + 1;
		else
			right = mid;
	}
	while (left < nums.size() && nums[left++] == target)
		res++;
	return res;
}

53-2. 0～n-1中缺失的数字

  • 一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

  • 输出

  • 输入: [0,1,3]

  • 输出: 2

  • 输入: [0,1,2,3,4,5,6,7,9]

  • 输出: 8

  • 方法：二分法，但是最后的判断很难。找到最左边不等于下标的数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int missingNumber(vector<int>& nums) {
	int left = 0;
	int right = nums.size() - 1;

	while (left < right) {
		int mid = left + right >> 1;
		if (nums[mid] != mid)
			right = mid;
		else
			left = mid + 1;
	}
	//如果从0 ~ n-1都不缺值, 则缺少的是n /  比如： 012,输出3
	return left == nums.size() - 1 && nums[left] == left ? left + 1 : left;
}

54.二叉搜索树的第k大节点

  • 给定一棵二叉搜索树，请找出其中第k大的节点。

  • 输出
    img1

  • 方法：利用搜索二叉树的中序遍历得到顺序数组

  • 方法：更加优秀的，直接利用倒置的中序遍历，反向从大到小开始遍历。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// int kthLargest(TreeNode* root, int k) {
//     vector<int>res;
//     help(root,res);
//     return res[res.size()-k];
// }

// void help(TreeNode* root,vector<int>& arr){
//     if(root==NULL)
//         return;
//     help(root->left,arr);
//     arr.push_back(root->val);
//     help(root->right,arr);
// }
//反向利用中序
int count = 0;
int res = 0;
int kthLargest(TreeNode* root, int k) {

	help(root, k);
	return res;
}

void help(TreeNode* root, int k) {
	if (root == NULL)
		return;
	help(root->right, k);
	if (++count == k)
		res = root->val;

	help(root->left, k);
}

55-1. 二叉树的深度

  • 输入一棵二叉树的根节点，求该树的深度。从根节点到叶节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度。

  • 输出
    img1

  • 方法：dfs求取树的深度

1
2
3
4
5
6
7
8
9
int maxDepth(TreeNode* root) {
	if (root == NULL)
		return 0;

	int lTree = maxDepth(root->left) + 1;
	int rTree = maxDepth(root->right) + 1;

	return lTree > rTree ? lTree : rTree;
}

55-2.判断是否平衡二叉树

  • 输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

  • 输出
    img

  • 方法：

  • DFS遍历看是否满足条件1：左中右和条件2：高度差不大于1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bool isBalanced(TreeNode* root) {
	//平衡二叉树——1.二叉搜索树2.左右子树高度差小于等于1
	if (root == NULL)
		return true;
	if (abs(depth(root->left) - depth(root->right)) > 1)
		return false;

	return isBalanced(root->left) && isBalanced(root->right);
}
int depth(TreeNode* root) {
	if (root == NULL)
		return 0;

	return max(depth(root->left), depth(root->right)) + 1;
}

拓展.二叉树路径和是否为Sum

img1

1
2
3
4
5
6
7
8
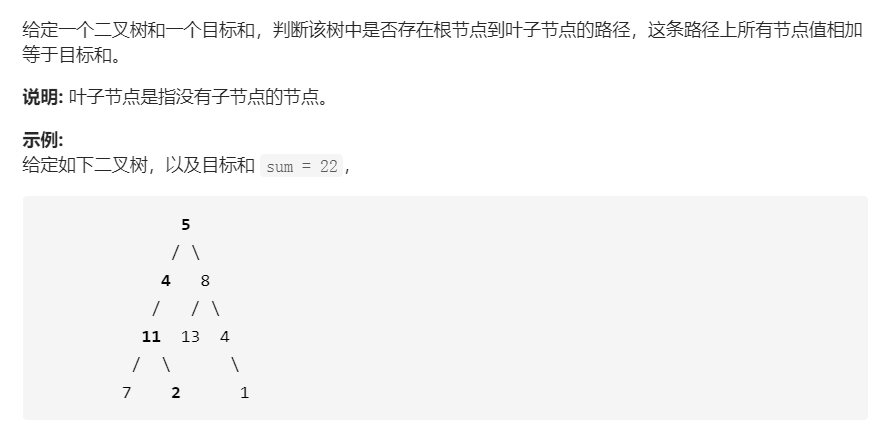
bool hasPathSum(TreeNode* root, int sum) {
	if (root == NULL)
		return false;
	if (root->left == NULL && root->right == NULL)
		return sum - root->val == 0;

	return hasPathSum(root->left, sum - root->val) || hasPathSum(root->right, sum - root->val);
}

拓展.求二叉树的最大直径

img1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int length;
int diameterOfBinaryTree(TreeNode* root) {
	length = 0;
	dfs(root);
	return length;
}
int dfs(TreeNode* root) {
	if (root == NULL)
		return 0;
	int L = dfs(root->left);
	int R = dfs(root->right);

	int curlength = L + R;
	length = max(length, curlength); //这个节点的最大值

	return max(L, R) + 1;            //返回该子节点的最大分治
}

56-1.数组中数字出现的次数

  • 一个整型数组 nums 里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n)，空间复杂度是O(1)。

  • 输出

  • 输入：nums = [4,1,4,6]

  • 输出：[1,6] 或 [6,1]

  • 输入：nums = [1,2,10,4,1,4,3,3]

  • 输出：[2,10] 或 [10,2]

  • 方法1：哈希表

  • 方法2：位运算

  • A^A=0

  • A&(-A)=最低一位

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
vector<int> singleNumbers(vector<int>& nums) {
	int sum = 0;
	//找出只出现一次的两个数,2和10
	for (auto it : nums)
		sum = sum ^ it;
	//根据两者的最低二进制差异位，区分两个数
	int flag = (-sum)&sum;
	vector<int>res(2, 0);
	//根据差异位来区分两组数,2一组,10一组
	for (auto it : nums) {
		if ((flag&it))
			res[0] ^= it;
		else
			res[1] ^= it;
	}
	return res;
}

56-2. 数组中数字出现的次数 II

  • 在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。

  • 输出

  • 输入：nums = [3,4,3,3]

  • 输出：4

  • 输入：nums = [9,1,7,9,7,9,7]

  • 输出：1

  • 方法1：哈希表

  • 方法2：位运算 / 出现几次就能被几整除，然后找到那个不能整除的位，累加

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int singleNumber(vector<int>& nums) {
	// unordered_map<int, int> mp;
	// for(int n : nums) mp[n] ++;
	// int ans;
	// for(auto pr : mp){
	//     if(pr.second == 1){
	//         ans = pr.first;
	//         break;
	//     }
	// }
	// return ans;
	int res = 0;
	for (int i = 0; i < 32; i++) {
		int temp = 0;
		for (auto it : nums) {
			if (it&(1 << i))temp++;
		}
		if (temp % 3 == 1)res ^= (1 << i);
	}
	return res;
}

57-1.数组中和为s的两个数字

  • 输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，则输出任意一对即可。

  • 输出

  • 输入：nums = [2,7,11,15], target = 9

  • 输出：[2,7] 或者 [7,2]

  • 输入：nums = [10,26,30,31,47,60], target = 40

  • 输出：[10,30] 或者 [30,10]

  • 方法：有序！！双指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
vector<int> twoSum(vector<int>& nums, int target) {
	//1.哈希表
	//2.双指针
	vector<int>res;
	int left = 0;
	int right = nums.size() - 1;

	while (left < right) {
		if (nums[left] + nums[right] < target)
			left++;
		else if (nums[left] + nums[right] > target)
			right--;
		else
			return { nums[left],nums[right] };
	}
	return res;

}

57-2.和为s的连续正数序列

  • 输入一个正整数 target ，输出所有和为 target 的连续正整数序列（至少含有两个数）。

  • 序列内的数字由小到大排列，不同序列按照首个数字从小到大排列。

  • 输出

  • 输入：target = 9

  • 输出：[[2,3,4],[4,5]]

  • 输入：target = 15

  • 输出：[[1,2,3,4,5],[4,5,6],[7,8]]

  • 方法：有序数组！！双指针区间的压缩和遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
vector<vector<int>> findContinuousSequence(int target)
{
	int i = 1;
	int j = 1;
	int sum = 0;//双指针缩放，连续空间
	vector<vector<int>>res;
	while (i <= target / 2) {
		if (sum < target) {
			sum += j;
			j++;
		}
		else if (sum > target) {
			sum -= i;
			i++;
		}
		else if (sum == target) {
			vector<int>temp;
			for (int u = i; u < j; u++) {
				temp.push_back(u);
			}
			res.push_back(temp);
			sum -= i++;
		}
	}
	return res;
}

58-1.翻转单词顺序

  • 输入一个英文句子，翻转句子中单词的顺序，但单词内字符的顺序不变。为简单起见，标点符号和普通字母一样处理。例如输入字符串”I am a student. “，则输出”student. a am I”。

  • 输出

  • 输入: “the sky is blue”

  • 输出: “blue is sky the”

  • 输入: “ hello world! “

  • 输出: “world! hello”

  • 解释: 输入字符串可以在前面或者后面包含多余的空格，但是反转后的字符不能包括。

  • 输入: “a good example”

  • 输出: “example good a”

  • 解释: 如果两个单词间有多余的空格，将反转后单词间的空格减少到只含一个。

  • 方法：利用stringstream ss(s)，但是当首字母有空的时候，还是直接使用>>；而不是getline

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
string reverseWords(string s) {
	if (s.size() == 0)
		return "";

	string res;
	stringstream ss(s);

	string temp;
	vector<string>arr;
	//getline(ss,temp,' ')
	while (ss >> temp) {
		arr.push_back(temp);
	}
	//很重要很重要
	if (arr.size() == 0) return "";

	for (int i = arr.size() - 1; i >= 1; i--) {
		res += arr[i] + " ";
	}
	res += arr[0];
	return res;
}

58-2.左旋转字符串

  • 字符串的左旋转操作是把字符串前面的若干个字符转移到字符串的尾部。请定义一个函数实现字符串左旋转操作的功能。比如，输入字符串”abcdefg”和数字2，该函数将返回左旋转两位得到的结果”cdefgab”。

  • 输出

  • 输入: s = “abcdefg”, k = 2

  • 输出: “cdefgab”

  • 输入: s = “lrloseumgh”, k = 6

  • 输出: “umghlrlose”

  • 方法：substr

1
2
3
string reverseLeftWords(string s, int n) {
	return  s.substr(n, s.size() - n) + s.substr(0, n);
}

59-1.滑动窗口的最大值——利用deque维护（连续区间）

  • 给定一个数组 nums 和滑动窗口的大小 k，请找出所有滑动窗口里的最大值。

  • 输出

  • 输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3

  • 输出: [3,3,5,5,6,7]

  • 解释:

  • 滑动窗口的位置 最大值

  • [1 3 -1] -3 5 3 6 7 3
  • 1 [3 -1 -3] 5 3 6 7 3
  • 1 3 [-1 -3 5] 3 6 7 5
  • 1 3 -1 [-3 5 3] 6 7 5
  • 1 3 -1 -3 [5 3 6] 7 6
  • 1 3 -1 -3 5 [3 6 7] 7

  • 方法：利用deque维护数组的最大值
    img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
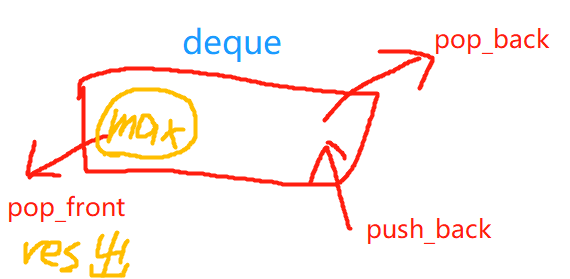
21
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
	int n = nums.size();
	deque<int> dq;
	vector<int> res;

	if (nums.size() == 0)
		return res;

	for (int i = 0; i < n; ++i) {
		while (!dq.empty() && i - dq.front() + 1 > k) {
			dq.pop_front();
		}
		while (!dq.empty() && nums[dq.back()] <= nums[i]) {
			dq.pop_back();
		}
		dq.push_back(i);
		if (i >= k - 1)
			res.push_back(nums[dq.front()]);
	}
	return res;
}

59-2.队列的最大值

  • 使得queue实现max_value、push_back 和 pop_front功能，同时摊时间复杂度都是O(1)。

  • 输出

  • 输入:

  • [“MaxQueue”,”push_back”,”push_back”,”max_value”,”pop_front”,”max_value”]

  • [[],[1],[2],[],[],[]]

  • 输出: [null,null,null,2,1,2]

  • 输入:

  • [“MaxQueue”,”pop_front”,”max_value”]

  • [[],[],[]]

  • 输出: [null,-1,-1]

  • 方法：queue正常元素入出，deque维护最大值的变化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
queue<int> que;
deque<int> dq;
int max_value()
{
	return que.empty() ? -1 : dq.front();
}

void push_back(int value)
{
	que.push(value);

	while (!dq.empty() && dq.back() < value)   //重要
		dq.pop_back();
	dq.push_back(value);
}

int pop_front()
{
	if (que.empty())
		return -1;
	int t = que.front();
	que.pop();

	if (t == dq.front())
		dq.pop_front();

	return t;
}

60.n个骰子的点数 （难）

  • 把n个骰子扔在地上，所有骰子朝上一面的点数之和为s。输入n，打印出s的所有可能的值出现的概率。

  • 你需要用一个浮点数数组返回答案，其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。

  • 输出

  • 输入: 1

  • 输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]

  • 输入: 2

  • 输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]

  • 方法：dp动态规划

1
2
3
4
5
6
7
8
9
10
11
12
vector<double> twoSum(int n) {
	vector<double> res(6 * n + 1, 0);
	res[0] = 1;
	for (int i = 1; i <= n; i++) {
		for (int j = 6 * i; j >= i; j--) {
			res[j] = 0;
			for (int x = j - 1; x >= i - 1 && x >= j - 6; x--) res[j] += res[x];
		}
	}
	for (auto &num : res) num /= pow(6, n);
	return vector<double>(res.begin() + n, res.end());
}

61.扑克牌中的顺子

  • 从扑克牌中随机抽5张牌，判断是不是一个顺子，即这5张牌是不是连续的。2～10为数字本身，A为1，J为11，Q为12，K为13，而大、小王为 0 ，可以看成任意数字。A 不能视为 14。

  • 输出

  • 输入: [1,2,3,4,5]

  • 输出: True

  • 输入: [0,0,1,2,5]

  • 输出: True

  • 方法：顺序遍历，相等return false；分类讨论；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
bool isStraight(vector<int>& nums) {

	sort(nums.begin(), nums.end());
	int king = 0;
	int diff = 0;
	for (int i = 0; i < nums.size() - 1; i++) {
		if (nums[i] == 0)
			king++;
		else {
			if (nums[i] == nums[i + 1])
				return false;
			else
				diff += nums[i + 1] - nums[i] - 1;
		}
	}
	return diff > king ? false : true;
}

62.圆圈中最后剩下的数字（约瑟夫环问题）

  • 0,1,,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。

  • 例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

  • 输出

  • 输入: n = 5, m = 3

  • 输出: 3

  • 输入: n = 10, m = 17

  • 输出: 2

  • 方法：约瑟夫环问题
    img
    img

1
2
3
4
5
6
7
8
int lastRemaining(int n, int m) {
	//约瑟夫环的问题
	int res = 0;
	for (int i = 2; i < n + 1; i++) {
		res = (res + m) % i;
	}
	return res;
}

63.股票的最大利润

  • 假设把某股票的价格按照时间先后顺序存储在数组中，请问买卖该股票一次可能获得的最大利润是多少？

  • 输出

  • 输入: [7,1,5,3,6,4]

  • 输出: 5

  • 解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。

  • 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。

  • 输入: [7,6,4,3,1]

  • 输出: 0

  • 解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。

  • 方法：动态方程

1
2
3
4
5
6
7
8
int maxProfit(vector<int>& prices) {
	int res = 0;
	for (int i = 1; i < prices.size(); i++) {
		res = max(res, prices[i] - prices[i - 1]);
		prices[i] = min(prices[i], prices[i - 1]);
	}
	return res;
}

64.求1+2+…+n

  • 求 1+2+…+n ，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

  • 输出

  • 输入: n = 3

  • 输出: 6

  • 方法：sizeof

1
2
3
4
int sumNums(int n) {
	bool arr[n][n + 1];
	return sizeof(arr) >> 1;
}

65.不用加减乘除做加法

  • 写一个函数，求两个整数之和，要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。

  • 输出

  • 输入: a = 1, b = 1

  • 输出: 2

  • 方法：位运算

1
2
3
4
5
6
7
8
9
int add(int a, int b) {
	while (b) {        //当没有进位则返回
		 // 注意leetcode中C++无法对int型最小值进行左移（所以转为无符号int型）
		int temp = (unsigned int)(a & b) << 1;//c:进位和————双1才1
		a ^= b;              //a:非进位和——单1才1
		b = temp;               //b = 进位
	}
	return a;
}

66.构建乘积数组

  • 给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B 中的元素 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。

  • 输出

  • 输入: [1,2,3,4,5]

  • 输出: [120,60,40,30,24]

  • 方法：先左后右

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> constructArr(vector<int>& a) {
	vector<int>res(a.size(), 0);

	int cur = 1;
	for (int i = 0; i < a.size(); i++) {
		res[i] = cur; //乘以左边的数
		cur *= a[i];
	}

	cur = 1;
	for (int i = a.size() - 1; i >= 0; i--) {
		res[i] *= cur;
		cur *= a[i];
	}
	return res;
}

67.把字符串转换成整数

  • 写一个函数 StrToInt，实现把字符串转换成整数这个功能。不能使用 atoi 或者其他类似的库函数。

  • 输出

  • 输入: “42”

  • 输出: 42

  • 输入: “space space -42”

  • 输出: -42

  • 输入: “4193 with words”

  • 输出: 4193

  • 输入: “-91283472332”

  • 输出: -2147483648

  • 解释: 数字 “-91283472332” 超过 32 位有符号整数范围。
    因此返回 INT_MIN (−231) 。

  • 方法：isdigit()函数，头文件cstdio

  • INT:INT_MAX \ INT_MIN

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<cstdio>

int strToInt(string str) {
	long res = 0;
	bool negative = true;
	int i = 0;
	while (str[i] == ' ')
		i++;

	if (!isdigit(str[i]) && str[i] != '+' && str[i] != '-')//非数字，正负号return
		return 0;

	if (str[i] == '-') {
		negative = false;
		i++;
	}
	else if (str[i] == '+') {
		negative = true;
		i++;
	}

	while (isdigit(str[i])) {
		res = res * 10 + str[i] - '0';
		if (negative == true && res > INT_MAX)
			return INT_MAX;
		if (negative == false && -res < INT_MIN)
			return INT_MIN;

		i++;
	}
	return negative ? res : -res;
}

68-1.二叉搜索树的最近公共祖先

  • 二叉搜索树

  • 输出
    img

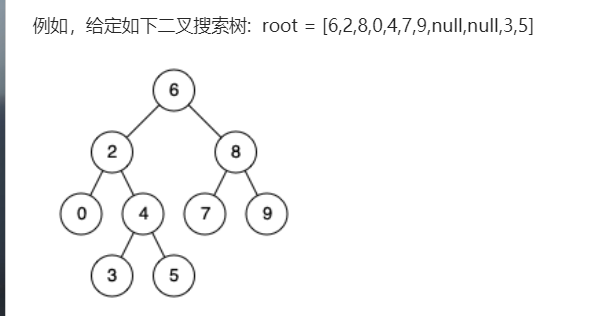
  • 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8

  • 输出: 6

  • 解释: 节点 2 和节点 8 的最近公共祖先是 6。

  • 输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4

  • 输出: 2

  • 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

  • 方法：利用特性：左中右

1
2
3
4
5
6
7
8
9
10
11
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
	if (root == NULL)
		return NULL;

	if (root->val > p->val &&root->val > q->val)
		return lowestCommonAncestor(root->left, p, q);
	if (root->val < p->val &&root->val < q->val)
		return lowestCommonAncestor(root->right, p, q);

	return root;
}

68-2.二叉树的最近公共祖先

  • 方法：

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
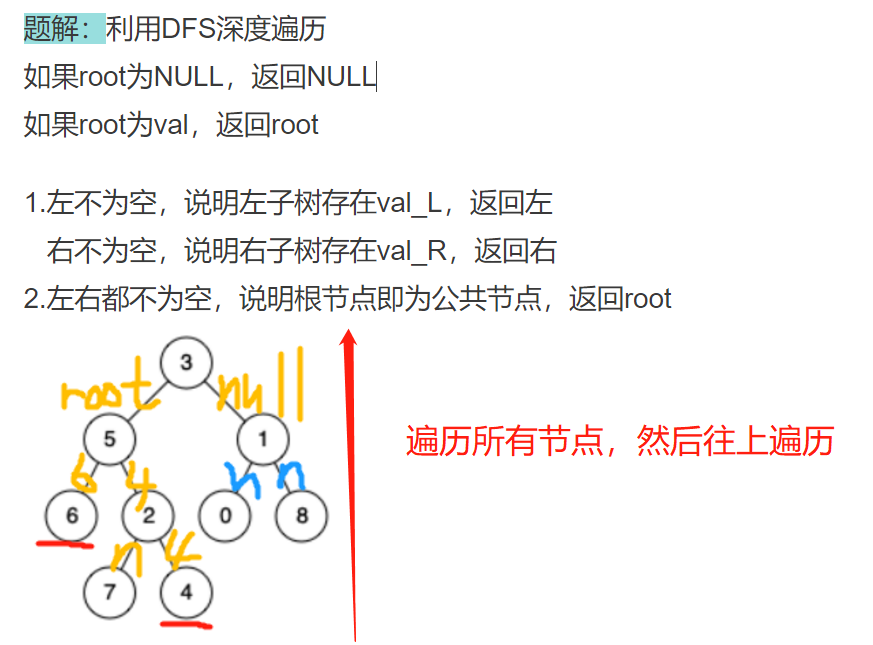
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
	if (root == NULL)
		return NULL;
	if (root == q || root == p)
		return root;
	TreeNode* L = lowestCommonAncestor(root->left, p, q);
	TreeNode* R = lowestCommonAncestor(root->right, p, q);

	if (L == NULL) return R;
	if (R == NULL) return L;
	if (L && R) return root;

	return NULL;
}
文章作者: Inter
文章链接: https://zuizichuan.cn/2020/07/20/jianzhioffer3/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Zichuan365' Blog！