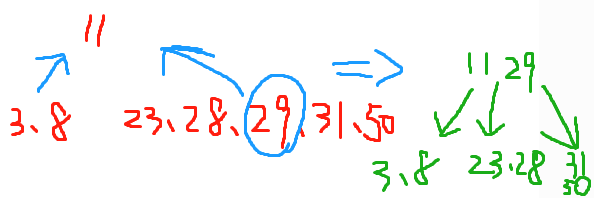Zichuan365' Blog HomeArchivesCategoriesGalleryAbout
C++ / 数据结构
|learn数据结构

哈希表（散列表）

1.定义

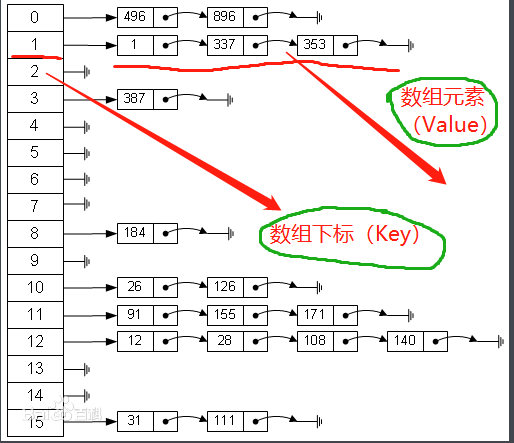
  • 哈希表是一种数据结构。一种Value数据内容和Key数据存放地址之间的映射关系。

  • 关键是Key和value值，我们通过Key值直接访问Value值

  • 这种反应映射关系的函数称为：散列函数 。存放数据的数组称为散列表。

img

2.作用以及优点和缺点

  • 我们需要一种快速寻址，插入删除方便的数据结构。

  • 数组是内存中的连续空间，寻址快速，插入删除困难。
  • 链表是内存中不连续的空间，寻址困难，插入删除快速。
  • 而哈希表是一种快速寻址，插入删除容易的数据结构。

优点和缺点

  • 优点：一对一查找高效 O(1)
  • 缺点：散列函数定义困难，散列冲突
  • 散列冲突：不同关键字，返回同个散列地址，散列函数定义困难
    • 优秀的散列函数 = 计算简单 + 分布均匀

  • 散列冲突的解决方案：

  1. 开放寻址法：当发现散列冲突后，按着顺序往下查找空余位置存放数据。简单来说就是进行二次探测。
  2. 链表法：在同一个Key对应的位置使用链表，从而达到存放多个数据的目的
    • 当链表太长时，长度大于8，我们可以使用红黑树进行降维。

3.应用

  1. 安全领域的加密算法：把一些不同长度的信息转化为杂乱128位的编码，编码值叫Hash值。
  2. 数据的快速查找：哈希表，又称散列，快捷的查找技术。原查找：A去和{532415646541A}比较 哈希查找：我知道了key值，直接去找对应位置的value值。
  3. 大数据处理中有着广泛的应用，提高查找的效率

4.常见的散列函数

  • 1.除法散列法
    index = value % 16 上表即是

  • 2.平方散列法

  • index = (value * value) >> 28 右移—转换为除法为2^28次

  • 数值分配均匀是可以的，但是value很大会溢出

  • 3.斐波那契散列法 / （黄金分割法）

  • 找到一个合理的乘数

  • 1，对于16位整数而言，这个乘数是40503

  • 2，对于32位整数而言，这个乘数是2654435769

  • 3，对于64位整数而言，这个乘数是11400714819323198485

  • 对于32位整数：

    • index = (value * 2654435769) >> 28

  • 散列表分布更加均匀

二叉搜索树（根本）

  • 左中右 / 左 < 中 < 右

平衡二叉树（AVL树）_O(logN)

1.作用

  • 平衡二叉树是基于二分法来提高数据查找速度的二叉树结构。

2.定义

  1. 二叉搜索树，遵循高度差原则（左右子树高度差不大于1）
    • 平衡因子：左子树高度 - 右子树高度，取值范围[-1，1]
    • 最小不平衡子树：距离插入节点最近的，打破平衡的子树。

3.平衡二叉树的元素插入

  • 当插入元素打破平衡二叉树平衡时（平衡因子变2），需要进行节点的调整。

  1. LL型——root节点左孩子的左孩子+新节点——打破平衡
  2. RR型
  3. LR型
  4. RL型

  • LL型（和RR型都是断开两个节点，然后平衡子树）
    img
    img
    img

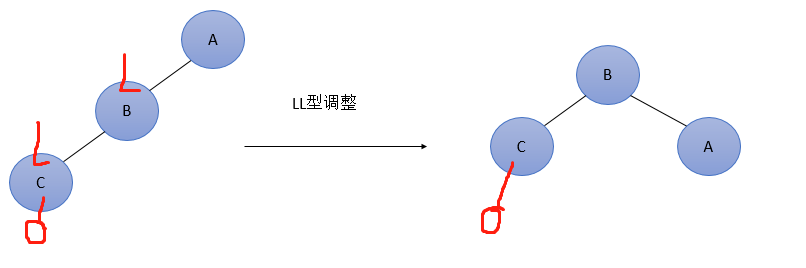
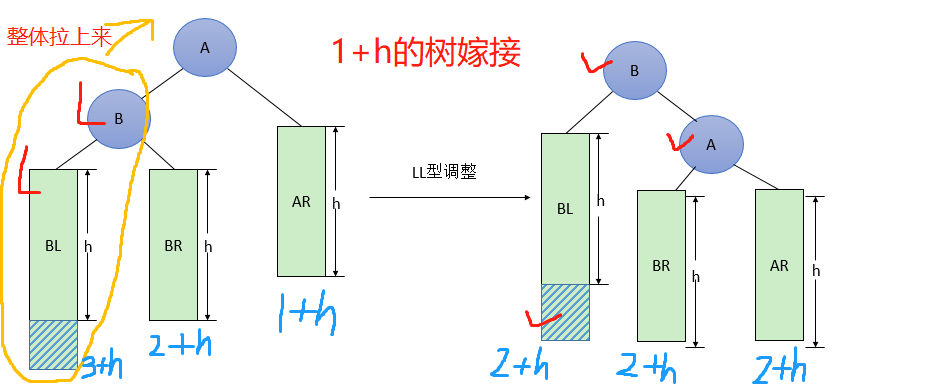
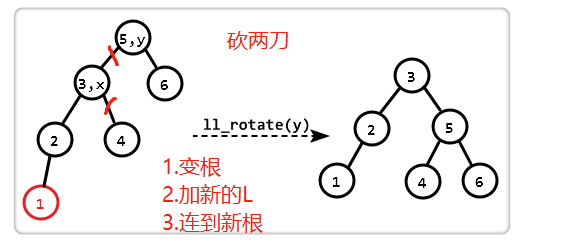
  • 和左孩子连接的两处，断开
  • 左孩子变成新根节点
  • 依次连接到左孩子上
1
2
3
4
5
6
7
8
9
10
BTNode *LL_rotate(BTNode *y) {
	BTNode *x = y->left;	//保存临时左孩子
	y->left = x->right;		//老根加新L
	x->right = y; 			//老根连到新根

	y->height = max(height(y->left), height(y->right)) + 1;  //计算变更后树的高度
	x->height = max(height(x->left), height(x->right)) + 1;

	return x;
}

  • RR型（和LL型类似）
    img

1
2
3
4
5
6
7
8
9
10
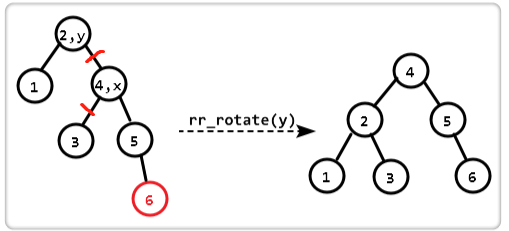
BTNode *rr_rotate(struct Node *y) {
	BTNode *x = y->right;	//保存临时右孩子
	y->right = x->left;		//老根加新R
	x->left = y;			//老根连到新根

	y->height = max(height(y->left), height(y->right)) + 1;
	x->height = max(height(x->left), height(x->right)) + 1;

	return x;
}

  • LR型（利用LL型和RR型）
    img
    img

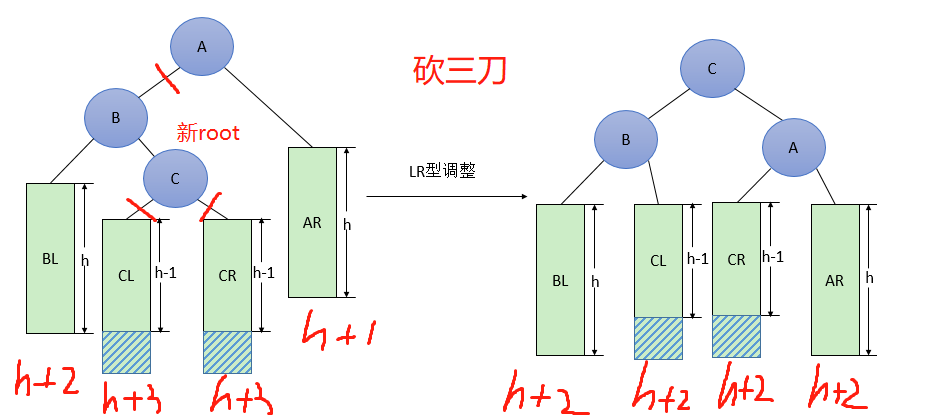
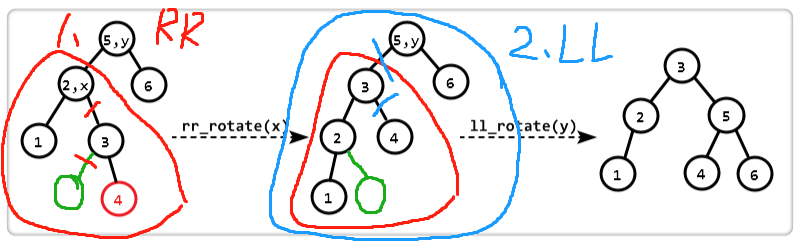
  • 断开三个节点，然后平衡子树，可以利用LL和RR来实现
  1. 先对左孩子RR旋转
  2. 再对整体LL旋转
1
2
3
4
5
BTNode* lr_rotate(BTNode* y) {
	BTNode* x = y->left;		//临时变量L节点
	y->left = rr_rotate(x);		//对根节点的左节点进行RR变换
	return ll_rotate(y);		//再对根节点进行LL变换
}

  • RL型（类似）
    img

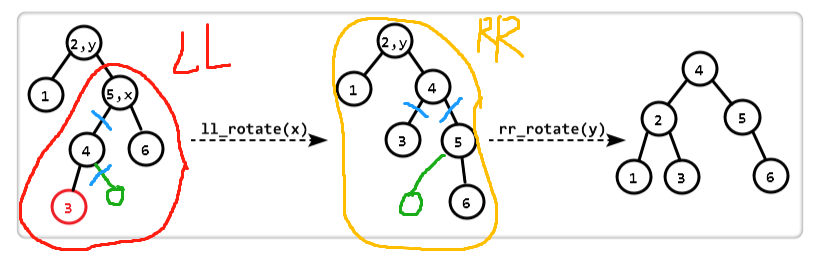
  1. 先对右孩子LL旋转
  2. 再对整体RR旋转
1
2
3
4
5
BTNode* rl_rotate(BTNode* y) {
	BTNode* x = y->right;		//临时变量R节点
	y->right = ll_rotate(x);	//对根节点的右节点的R节点进行LL变换
	return rr_rotate(y);		//对根节点进行RR变换
}

4.平衡二叉树的特点

  1. 查找元素所花时间不固定，平均log2n。
  2. 高度平衡，维护代价比较高，需要不断的旋转二叉树保持稳定。

红黑树_O(logN)

性质

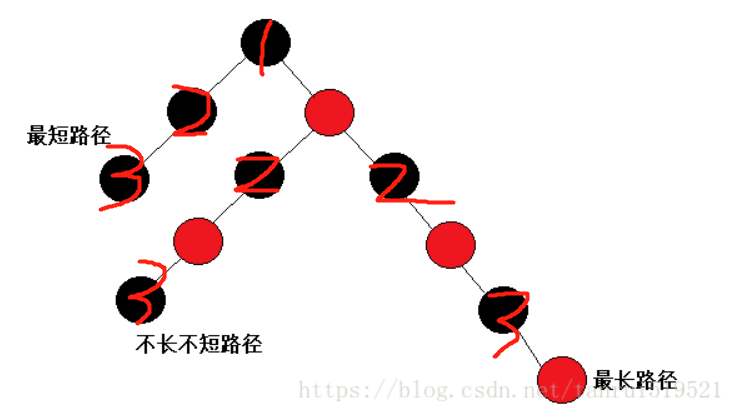
  • 关键性质：从根结点出发，每条路径最大差异为一倍，所以保证了红黑树大致的平衡

  • 极限情况：max = 2 * min

1.定义

  • 二叉搜索树，同时遵循红定理和黑定理

    • 没有连续的红色节点
    • 所有路径上黑色节点个数相同Sum（根节点为黑色）

img

2.红黑树的旋转后、重新着色（插入）

  • 旋转较少，维护比较容易

  • 我们默认插入的是红色节点，因为默认插入黑色节点时，开销太大。

  1. 当父节点为黑色，直接插入
  2. 当父节点为红色，祖父节点必为黑色。
    1. 叔叔存在且红——父亲变黑色节点，然后根据颜色变化继续向上调整，左旋 / 右旋。
    2. 叔叔存在且黑——和叔叔交换，并调整位置满足二叉搜索树
    3. 叔叔不存在——占据叔叔位置，并调整位置满足二叉搜索树

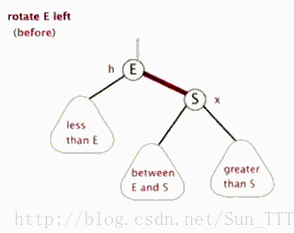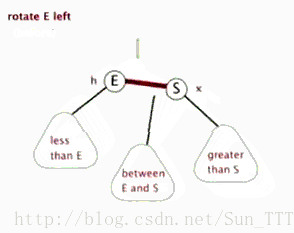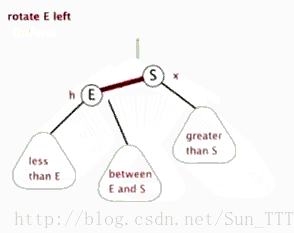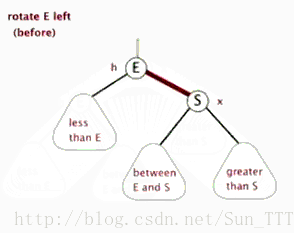
3.红黑树的左旋和右旋（需要指定父节点）

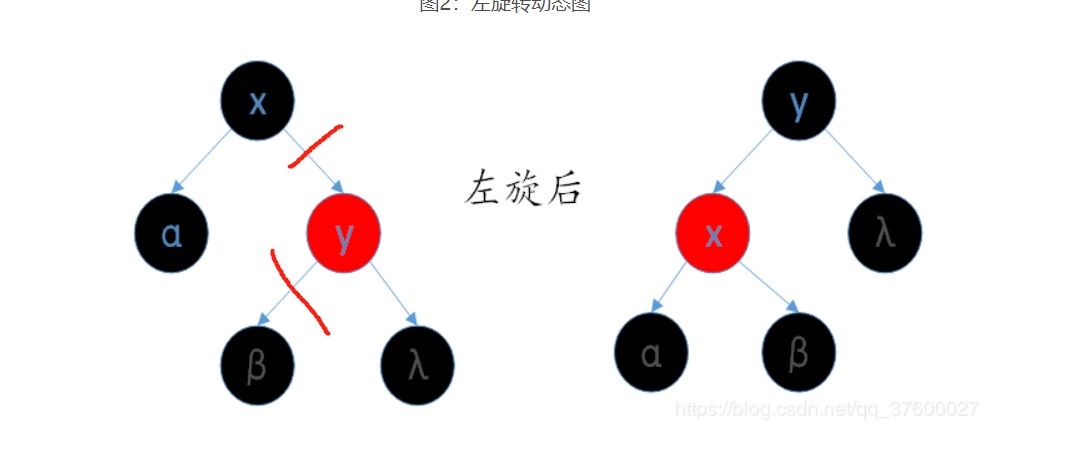
  • 左旋

  • 类似平衡二叉树的RR旋转，加上每个节点还有指向父节点指针。
    img
    img
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    void Left_Rotate(BiTreeNode* root, BiTreeNode* x)
    {
    	//1
    	BiTreeNode* y = x->rightChild;
    	//2
    	x->rightChild = y->leftChild;

    	//指定父节点
    	y->leftChild->p = x;
    	y->p = x->p;

    	//指定新root的根节点
    	if (x->p == NULL)
    		root = y;
    	else if (x->p->leftChild == x)
    		x->p->leftChild = y;
    	else
    		x->p->rightChild = y;

    	//3
    	y->leftChild = x;
    	//指定父节点
    	x->p = y;
    }

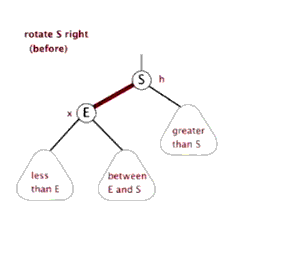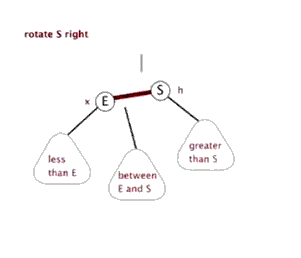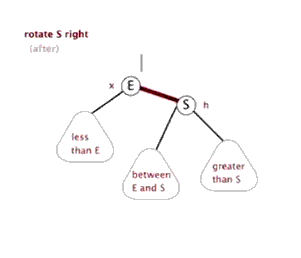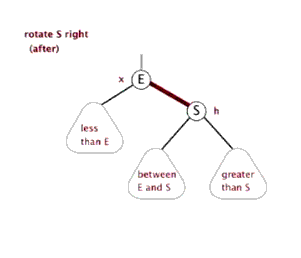
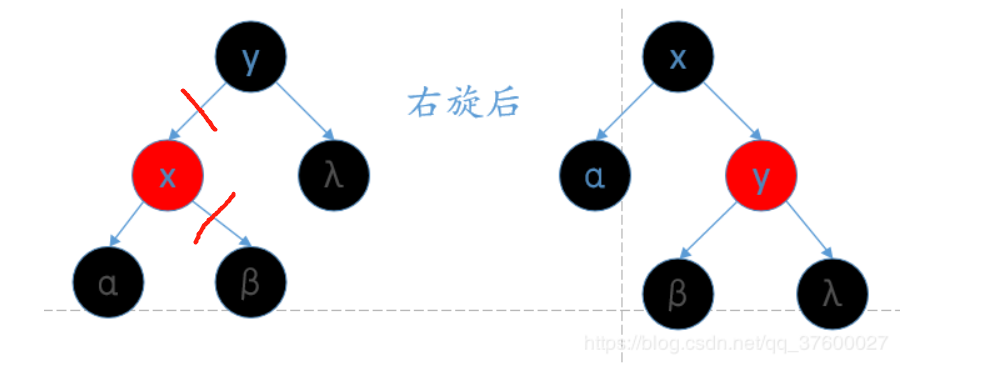
  • 右旋

  • 类似平衡二叉树的LL旋转，加上每个节点还有指向父节点指针
    img
    img
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    void Right_Rotate(BiTreeNode* root, BiTreeNode* y)
    {
    	//1
    	BiTreeNode* x = y->leftChild;
    	//2
    	y->leftChild = x->rightChild;
    	//指定父节点
    	x->rightChild->p = y;
    	x->p = y->p;

    	//指定新root的根节点
    	if (y->p == NULL)
    		root = x;
    	else if (y->p->rightChild == y)
    		y->p->rightChild = x;
    	else
    		y->p->leftChild = x;

    	//3
    	x->rightChild = y;
    	//指定父节点
    	y->p = x;
    }

B树 / B+树 / B*树特点（单节点多Value）

  1. B树 = 单节点多Value
  2. B+树 = 仅叶子节点保存Value值，底层有序链表相连。
  3. B* 树 = B+树 + 再在其枝节点加上兄弟节点指针。

B树

1.特点：单节点多Value，树的层数更低

2.定义——H树的阶数

根据阶数H定义

  1. 满足二叉搜索树
  2. 叶子节点同层
  3. 节点的关键字数量（Value）：【ceil(H/2) - 1，H - 1】(叶子无限制)
  4. 节点的索引指针数量（left、right） 【2 ， H】，即索引指针

  • 子节点：除了叶子的（left、right）

  • 枝节点：除了根和叶子的（value）

  • 简单来说

  1. 满足二叉搜索树
  2. 节点的Value值和left、right指针发生了变化，一个节点不单单包含一个Value值。

img

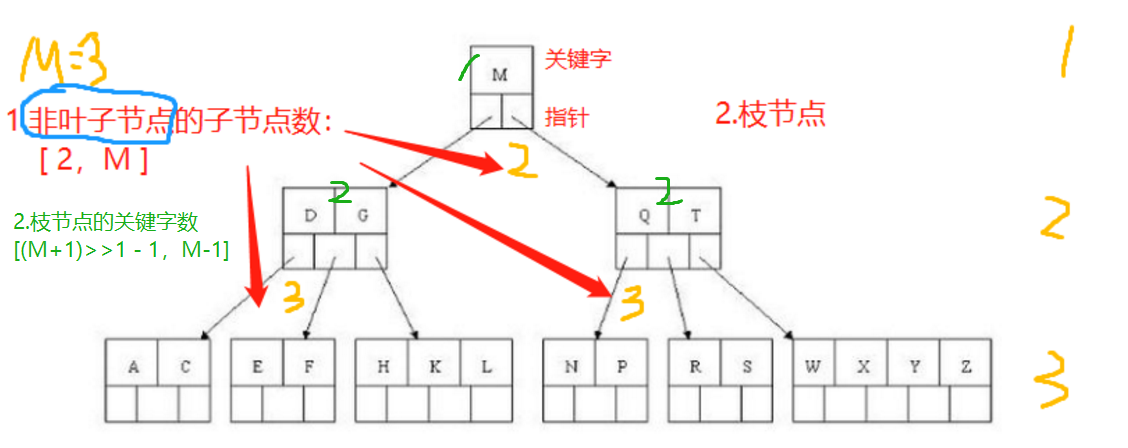
3.元素的插入和删除

  • 当我们树的高度H = 5时

  • left/right数量——[2,5]——索引指针（肯定比Value数量+1）

  • value数量——[2,4]——枝节点

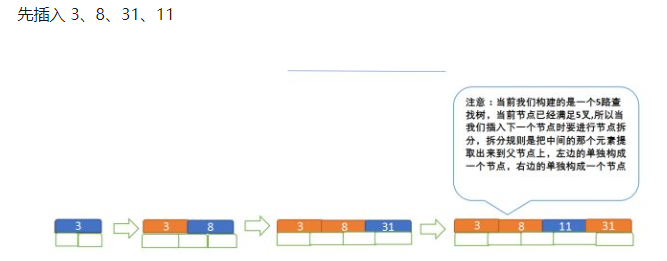
  • 插入构造图示：

  • A：先插入4个数，当插入地5个时，不满足了关键字数，所以需要拆分

    • img

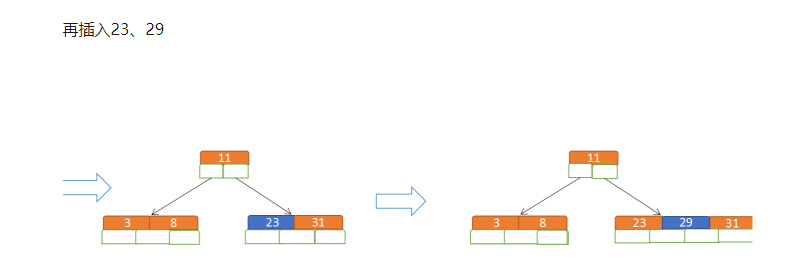
  • B：再插入23、29，此时区中间元素，将元素分为左中右三块

    • img

  • C：再插入50、28，此时区中间元素，将元素分为左中右三块

    • img

  • 删除构造图示：为了满足value树[2,4]

  • img

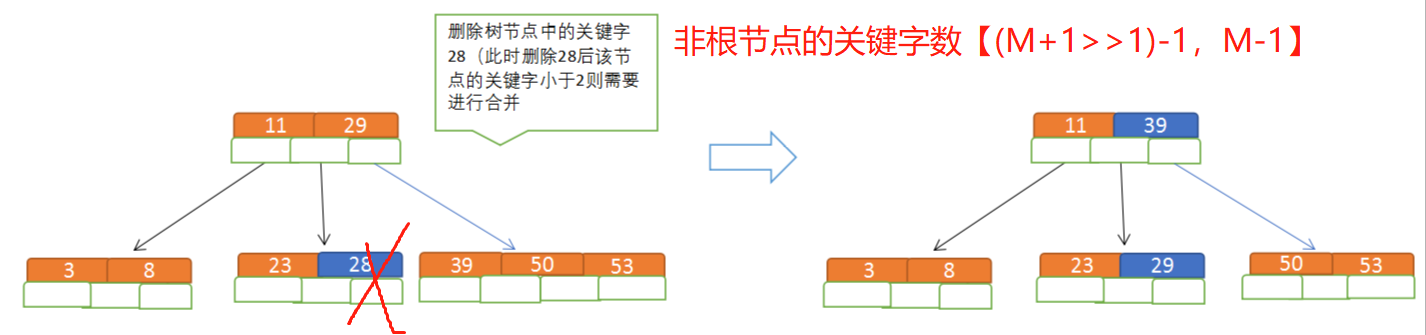
4.特点

  • 相比于平衡二叉树，每个节点的关键字增加了，树的层级变少了，减少了数据查找的次数和复杂度。

B+树

1.特点

  • B树的升级版本，更加充分的利用节点的空间

2.定义

  1. 叶子节点保存Value值，其他节点只进行数据索引
    • 非叶子节点可保存的数据量大大增加
    • 所有查询时间相同
  2. 叶子节点Value值按顺序保存，同时底层叶子节点保存右边节点指针
    • 类似顺序链表，首尾相连，便于区域数据的查询
  3. Value值和索引指针数量相同，而B树索引指针数量 = Value值数量 + 1

  • 定义图示
    img

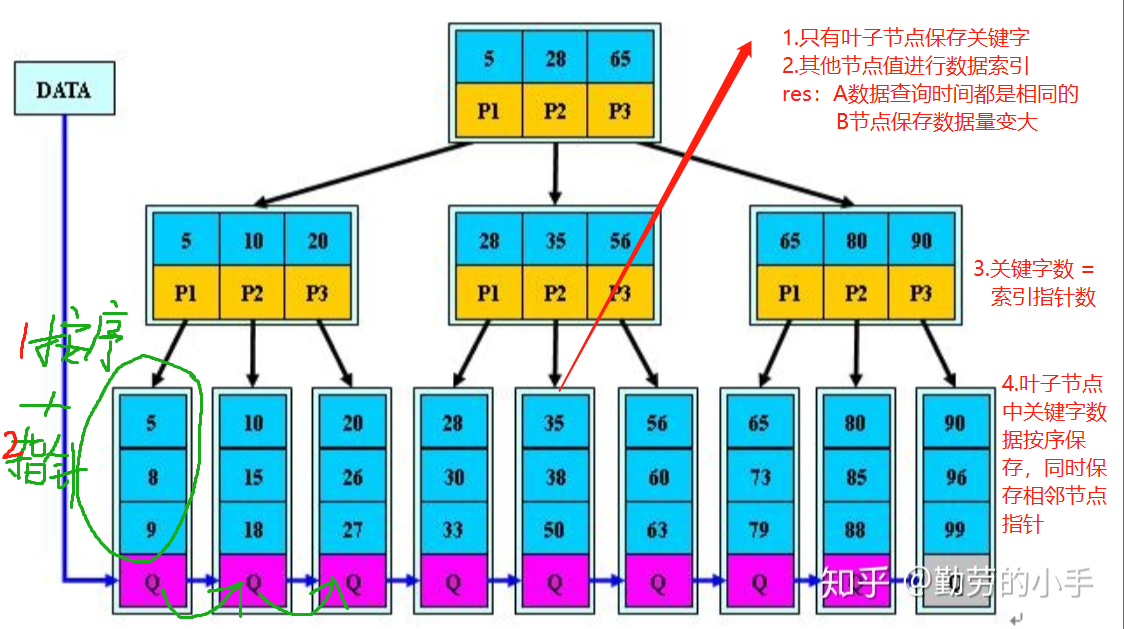
3.特点

  1. 枝节点只进行数据索引，不保存关键字的指针。
    • 枝节点存放的信息越多，层级更少。
  2. 所有Value值都在叶子节点上，查询更稳定。
  3. 底部数据构成了一个有序链表，查询区间数据更加方便。

B*树

和B+树的区别

  • B* 树是B+树的升级版本，枝节点增加增加指向兄弟节点的指针。
    img

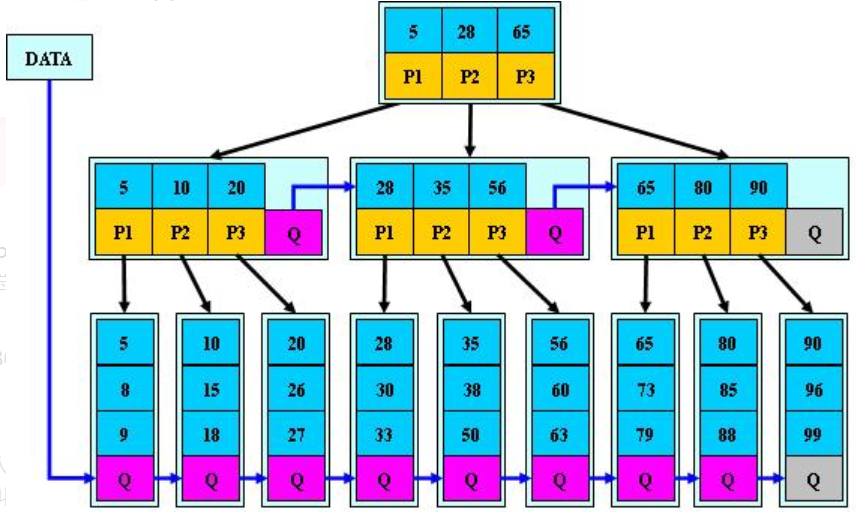
特点

  • 节点的分裂不同
    • B+树：一半元素放置到新节点上，父节点增加新节点的索引指针。
    • B* 树：
      • 1.首先查询兄弟节点是否空余，空余直接移至兄弟节点。
      • 2.兄弟不空余，原节点和兄弟节点插入新节点，移动1 / 3元素至新节点，改变对应关键字。

优点

  • 将节点的最低利用率从1/2提升到2/3，B* 树比B+树分配新节点的概率要低，空间使用率更高。

  • 节点的利用率更高，从1/2变成2/3，新节点的分配概率更低。

所有树的总结

1.All树

  • 二叉树搜索树

  • 左<中<右的顺序关系

  • 平衡二叉树

  • 满足二叉搜索树
  • 子树的高度差不大于1
  • 特点：平衡二叉树是基于二分法来提高数据查找速度的二叉树结构，维护成本高。

  • 红黑树

  • 满足二叉搜索树
  • 满足红定理和黑定理（无连续红、路径黑Sum相同、根节点黑）
  • 特点：黑定理保证了红黑树大致的平衡，同时无需高强度的旋转，维护成本较低。

  • B树（单节点多Value）

  • 满足二叉搜索树

  • 每个节点的Value值和索引指针不再局限于1个和2个，每个节点可以存放更多的数据，层数更低，查找时间更短。

  • 索引指针【2 ， H】，Value【 ceil(H) - 1，H - 1 】向上取整

  • 特点：每个节点的Value值和索引指针不再局限于1个和2个，每个节点可以存放更多的数据，层数更低，查找时间更短。

  • B+树（Value全在叶子节点 + 底层顺序链表）

  • B树的升级版本，只有叶子节点保存Value值，其他节点只进行数据索引
  • 底层链表相连，枝节点Value值和索引指针一一对应。
  • 特点：查询时间稳定，同时枝节点可以保存更多的节点信息，层数降低。底层有序链表，查询区间数据更便捷。

  • B* 树

  • B+树的基础上增加枝节点的兄弟指针，节点利用率1/2，变成2/3，分配新节点的概率更低。

2.B树三种树的优劣 / Important

  • B树：单节点多value值和多索引指针，当经常访问的关键字靠经根节点时，B树查询速度较快。
  • 而B+树只有叶子节点保存Value值，其他节点只作数据索引：更加稳定，层级较少，每次查询的时间相同。同时底部数据是连续链表，适合查询一段区间的数。
  • 而B* 树在B+树的基础上增加了非叶子节点的兄弟节点指针，分配新节点的概率低，在元素分裂的时候移动元素为1/3，比B+的1/2空间利用率更高。

3.拓展：Trie字典树（前缀树 / 空间换时间）

  • Trie字典树：又称前缀树，利用公共前缀来提高降低查询所需的时间。典型的空间换时间。
  • 主要用于排序和统计大量的字符串，经常被搜索引擎用于频繁词的统计。
  • 优点：最大限度地减少无谓的字符串比较，查询效率比哈希表高。
  • Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

问题问题

1.说一下平衡二叉树和红黑树的定义、特定、区别

  • 平衡二叉树,又名AVL树，是基于二分法的而创立的便于数据查找的数据结构。

  1. 他是一棵二叉搜索树，同时满足高度定理。就是所有节点的子树高度差不大于1。
  2. 插入和删除的时间复杂度都是O（log2n），由于其高度平衡，所以维护成本很高，一直需要旋转，从而满足平衡二叉树结构。
    • 主要有四种旋转LL、RR、LR、RL旋转。

  • 红黑树,简称RB树，是一棵加了颜色信息的二叉树。

  1. 他同样也是一棵二叉搜素树，同时满足红定理和黑定理。

    • 红定理就是其没有连续的红色节点。
    • 黑定理就是其每个节点的路径上的黑色节点数是相同的。这个性质保证了红黑树的大致平衡性。

  2. 插入和删除时没有平衡二叉树那么多的旋转。同时我们默认插入的是红色节点，所以有4种情况。

  • 1.父亲为黑直接满足
  • 2.父亲为红，那么爷爷肯定为黑，我们只需要讨论叔叔节点即可。
  1. 旋转主要有左旋和右旋，最多旋转三次，就能恢复红黑树的性质。

  • 总结：红黑树放弃了平衡二叉树的高度平衡，追求大致平衡。

  • 平衡二叉树频繁插入和删除操作，需要频繁的旋转，导致效率下降。
  • 而红黑树每次插入最多只需要三次旋转就能达到平衡，实现较为简单，所以运用比较广泛，如STL种的Set和Map容器底层都是红黑树。

2.平衡二叉树AVL、红黑树、B树的运用场景

  • 1.平衡二叉树运用较少，维护代价较高：window对进程的地址管理运用到了平衡二叉树

  • 2.红黑树：广泛运用于C++中STL中，set和map底层都是红黑树

  • 3.B/B+树：用于磁盘文件索引、数据索引、数据库索引等

3.请你说一下哈夫曼/霍夫曼编码

  • 霍夫曼编码是霍夫曼树的一种应用，广泛应用于文件压缩。
  • 其使用字符出现的频率，建立霍夫曼树，路径上的0和1来表示字符。

4.Map / Set的底层为什么用红黑树

  • AVL 树是高度平衡的，频繁的插入和删除，会引起频繁的旋转，导致效率下降，维护成本很高。
  • 红黑树放弃了高度平衡的树，同时他满足黑定理，红定理，保证了他大致上也是平衡的。而插入和删操作最多三次旋转，效率较高，维护成本低。

5.说一下B树

  • 首先B树也是一个二叉搜索树，他和红黑树以及平衡二叉树的最大区别在于：他单节点可以多Value值和多索引指针。

  • Value值和索引指针的数量取决于树的阶数，索引指针一般为【2，H】，Value值为【ceil(H/2)-1，H-1】(枝节点)
  • 这样导致B树有很大的优点：就是节点储存的信息更多了，树的层数降低了，节点的利用和访问更加高效。
  • 被广泛的运用于磁盘文件索引、数据索引、数据库索引等。

6.说一下B+树

  • B+树是B树的变形，他只在叶子节点储存Value值，枝节点只保存索引指针。同时底层用有序链表相连。

  • 这样导致B+树搜索数据的时间是稳定的，同时枝节点可以保存更多的信息。底层的有序链表便于对于区间数据据的查询。

7.请你说一下map和unordered_map的底层实现

  • map底层是红黑树实现的，因此map中元素排列是有序的。

  • underordered_map是哈希表实现的，所以其元素是无序的，由对应的KeyValue对应值对应。

  • map：有顺序要求

  • 优点：有序性，这是map结构最大的优点，

  • 缺点：查询速度慢，占用空间大

    • 其每个节点需要**保存父节点，
    • 同时需要相应的反转操作**。

  • unordered_map：无顺序要求

  • 优点： 因为内部实现了哈希表，因此其查找速度非常的快

  • 缺点： 建立哈希表比较困难，建立合适的散列函数比较困难。

8.请你说一下红黑树的性质还有左右旋转

  • 红黑树是在平衡二叉树基础上提出来的，由于平衡二叉树的高度平衡性，使得插入删除等操作旋转次数过多，开销太大。

  • 而红黑树相较于平衡二叉树，不需要频繁的旋转，最多旋转三次便可满足所有条件，同时满足黑定理和红定理大致上也相对平衡。

  • 红黑树的性质:

  • 满足：红定理和黑定理

  1. 其满足二叉搜索树
  2. 红定理：无连续的红色节点
  3. 黑定理：根节点为黑，每条路径上黑色节点个数相同。

  • 红黑树的旋转：旋转以后，变换颜色。直至满足。

  • 一般插入最多旋转2次，删除3次就可以满足，然后变换颜色。
  • 左旋：类似平衡二叉树的RR旋转，同时重新定义指向父节点的指针。
  • 右旋：类似平衡二叉树的LL旋转，同时重新定义指向父节点的指针。
  • 我们默认插入的节点颜色是红色，这样父亲是黑色，只需要讨论叔叔节点的情况即可。

9.Stack overflow/栈溢出，举个简单的例子导致栈溢出

  • 变量写入的字节数，超过了申请的字节数。

  • 数组越界

  • 栈溢出原因：

  1. 临时变量大小过大。
    • 解决：增大栈空间，或者使用malloc和new动态分配内存空间
  2. 递归调用层次太多。递归函数在运行时，会进行压栈操作，压栈次数太多会导致栈溢出。
  3. 指针或者数组越界。

10.栈和堆的区别，为什么栈快

  • E栈区—存放函数局部变量，形参和函数返回值等（最快）

  • D堆区—存放 malloc 和 new 、自己开辟的内存，程序员手动开辟和释放

  • C静态区（全局区）—存放静态变量和全局变量

    • DATA段：全局初始化区
    • BSS段：全局未初始化区

  • B文字常量区—存放常量，如：10，字符串常量等等

  • A代码区—存放程序的代码区

  • 栈：由高地址往低地址扩展，系统自动管理，自动优化。系统停供支持，分配效率高。

  • 堆：由低地址往高地址扩展，由程序员手动申请释放内存，多了很多步骤，存在内存碎片，分配效率低，所以较之栈慢。

  • 同时栈位于一级缓存中，堆在二级缓存中做缓存。

11.说一下数组和链表的区别

  • 数组是元素在连续内存空间，支持随机访问，寻址快速，但是删除插入效率低。而且固定不能动态扩展。

  • 链表中元素不是连续存储的，通过指针关联，插入删除快，内存利用率高，大小灵活。但是寻址快速困难，不支持随机访问。

文章作者: Inter
文章链接: https://zuizichuan.cn/2020/07/28/C-%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84-1/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Zichuan365' Blog！