Zichuan365' Blog HomeArchivesCategoriesGalleryAbout
LeetCode / 十大排序
|LeetCode十大排序算法

优质资源：https://www.cnblogs.com/onepixel/p/7674659.html

img

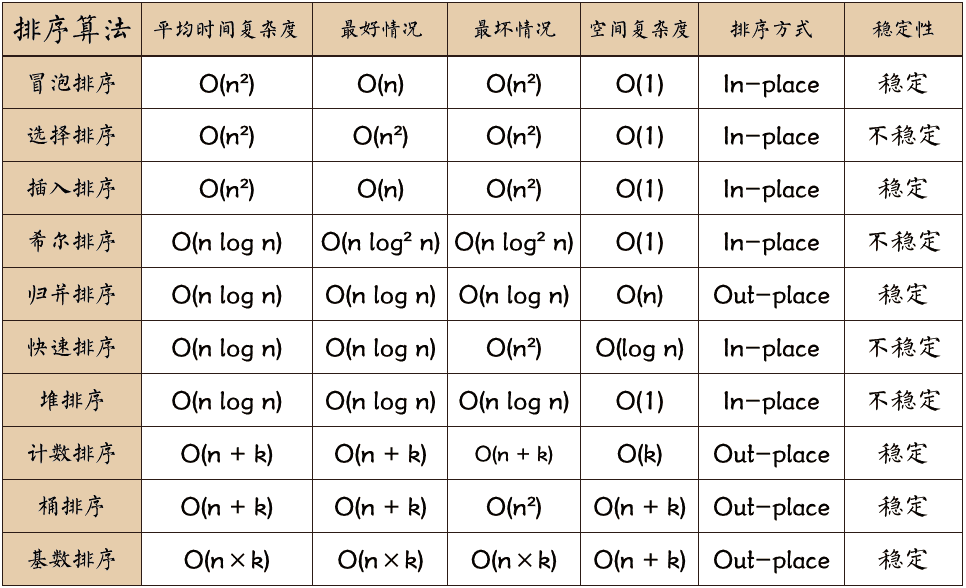
比较类排序

  • 排序算法稳定：稳不稳定看交换过程中，相同的元素会不会改变前后顺序

  1. 冒泡排序：稳定
  2. 选择排序：不稳定，5、8、5、2、6，第一趟下来5和5的前后顺序改变
  3. 插入排序：稳定
  4. 希尔排序：不稳定，因为增量为gap的排序，排的过程中可能已经发生了变化。
  5. 归并排序：稳定，分治。（前后顺序不变）
  6. 快速排序：不稳定，元素左右交换时，会发生改变
  7. 堆排序：不稳定，构造堆时发生改变

冒泡，插入、归并

  • 稳定：冒泡，插入、归并、非比较类排序

冒泡，插入、归并

  • 不稳定：选择、希尔、快排、堆

1.冒泡排序

  • 直接两两比较，n次遍历，进行进行交换，将最大的元素移至最后。
    时间复杂度O(n^2)、空间O(1)

img

1
2
3
4
5
6
7
8
9
10
11
12
13
//1.冒泡------------逐步把最大的放后面去
void sort(vector<int>& arr)
{
	for (int i = 1; i < arr.size() ; i++) {
		for (int j = 1; j < arr.size() - i; j++) {
			if (arr[j-1]  >  arr[j]) {
				int temp = arr[j];
				arr[j] = arr[j - 1];
				arr[j - 1] = temp;
			}
		}
	}
}

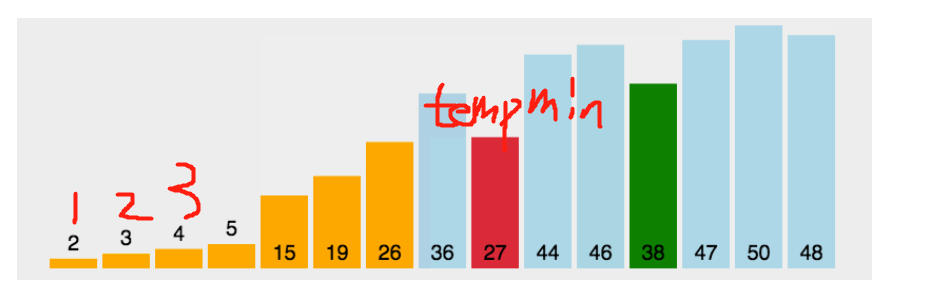
2.选择排序

  • 不直接交换，两两比较，进行下标的交换，记录最小元素下标

时间复杂度O(n^2)、空间O(1)

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
//2选择--------------记录最小元素下标、然后进行元素交换
void sort(vector<int>& arr)
{
	for (int i = 0; i < arr.size(); i++){
		int tempIndex = i;
		for (int j = i;j < arr.size(); j++)
		{
			if ( arr[j] < arr[tempIndex]){
				tempIndex = j;
			}
		}
		int temp = arr[i];
		arr[i] = arr[tempIndex];
		arr[tempIndex] = temp;
	}
}

3.插入排序

  • 增量为1，选取一个元素，将他元素插入到合适的位置。

时间复杂度O(n^2)、空间O(1)

img

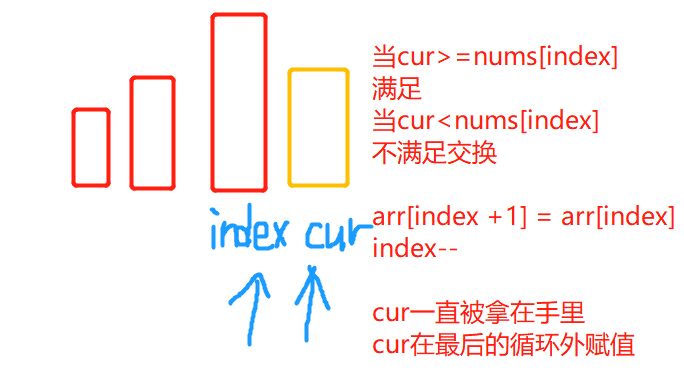
cur是被挂起的，最后进行赋值 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
//3插入排序--------------增量为1的希尔排序
//逐渐交换    总数比较：2   3   4
//int cur  = index[i]
//index = i - 1;
//然后逐渐往前进行比较：之前的数组已经排序好了，所以把cur放在合适它的位置即可

//将cur放在它的合适位置即可
void sort3(vector<int>& arr)
{
	for(int i = 1;i<arr.size();i++){
		int cur = arr[i];	//当前元素
		int index = i - 1;  //当前元素的前一下标
		
		while(index >=0 && arr[index] > cur)
		{
			arr[index + 1] = arr[index];
			index--;
		}
		arr[index + 1] = cur;
	}
}

4.希尔排序

  • 增量为n的插入排序，当元素总体上有序时，插入排序很高效，所以先大致排序整齐。

时间复杂度O(n * logN)、空间O(1) 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//4.希尔排序，增量为gap的插入排序，先使其大致有序，然后再以增量减小的方式排序

//插入排序在数组基本有序的情况下，效率是很高的。所以缩小增量排序--希尔排序
void sort4(vector<int>& arr) {
	int len = arr.size();
	for (int gap = len / 2; gap >= 1; gap /= 2) {
		for (int i = gap; i < arr.size(); i += gap) {
			int cur = arr[i];
			int index = i - gap;
			while (index>=0 && cur<=arr[index])
			{
				arr[index + gap] = arr[index];
				index -= gap;
			}
			arr[index + gap] = cur;
		}
	}
}

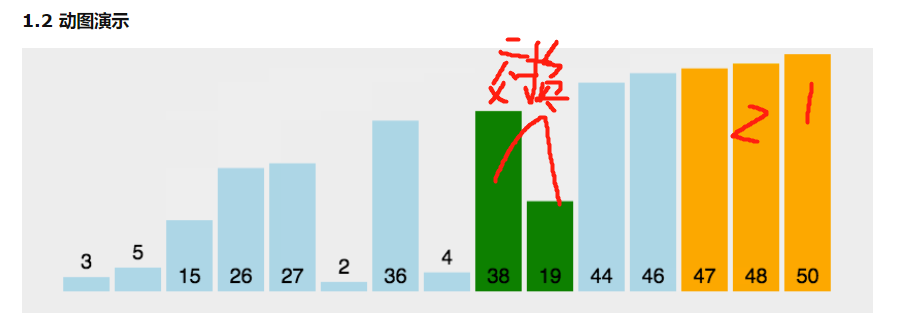
5.归并排序

  • 先分再和，先将元素分成单个个体，然后两两组合，最后合并成一个有序数组

  • 先分再和，双指针一次将元素填入位置

时间复杂度O(n * logN)、空间O(N)

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
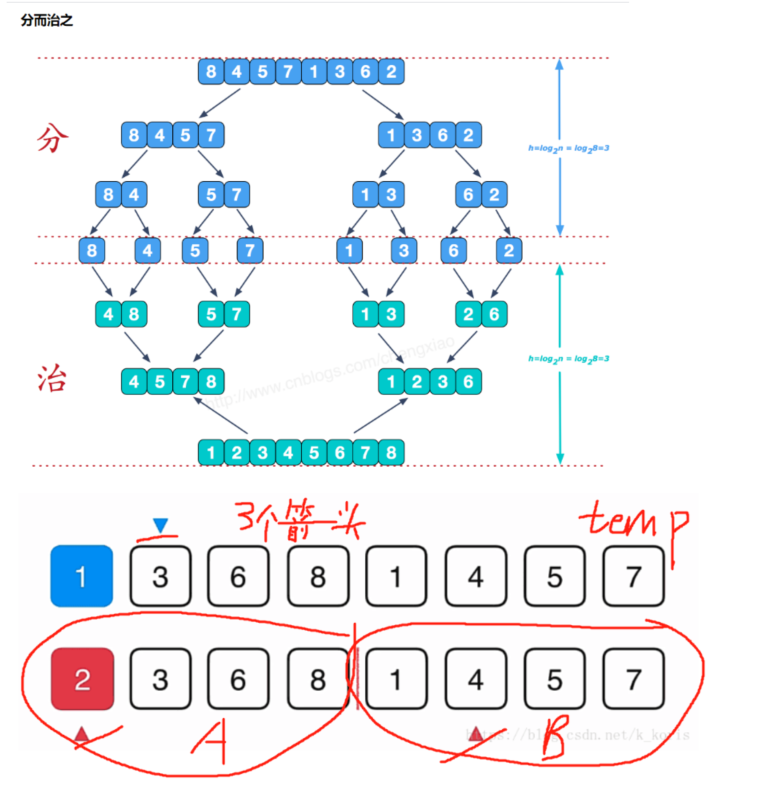
//5.归并排序---分而治之的思想，先将元素分组，然后22相结合排序
//先分，然后组合
void merge(vector<int>&arr, vector<int>&temp, int L, int mid, int R) {

	int p1 = L;
	int p2 = mid + 1;
	int p = L;
	while (p1 <= mid && p2 <= R) {
		if (arr[p1] <= arr[p2]) 
			temp[p++] = arr[p1++];
		else
			temp[p++] = arr[p2++];
	}
	while (p1 <= mid) temp[p++] = arr[p1++];
	while (p2 <= R)   temp[p++] = arr[p2++];

	copy(temp.begin() + L, temp.begin() + R + 1, arr.begin() + L);
}

//额外空间传入vector<int>&tmp，空间大小：O(n)
void sort(vector<int>&arr, vector<int>&tmp, int L, int R) {
	if (L >= R)
		return;

	int mid = (L + R) / 2;
	sort(arr, tmp, L,  mid);
	sort(arr, tmp, mid + 1, R);

	merge(arr, tmp, L, mid, R);
}

6.快速排序

  • 先和再分，以第一个元素为基准数，大的放右，小的放左，然后依次再以基准数排序

  • 注意：这里包含往下取整还是往上，注意

    1
    2
    3
    4
    while(arr[p2] >temp && p1 < p2)
    	p2--;
    while (arr[p1] <temp && p1 < p2)
    	p1++;
    时间复杂度O(n * logN)、空间O(logN)

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
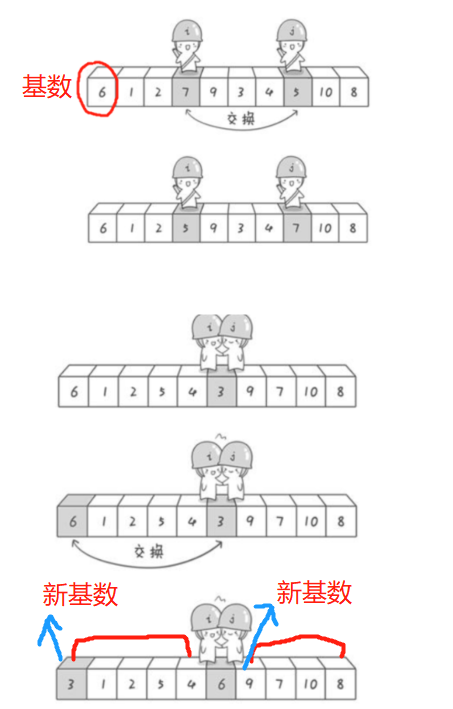
//6.快速排序---以不同的基数，将其分组，分别排序
//一开始以第一个数，作为基数，大于放在右边小于放在左边
//然后继续左右两组在此快速排序

//空间复杂度：最优——O（log2n）（平分数组）、最差——O（n）（平分数组）
void sort6(vector<int>&arr, int L, int R) {
	if (L >= R)
		return;

	int cur = arr[L];
	int p1 = L, p2 = R;
	int p = 0;

	while (p1 < p2) {
		while (arr[p2] >= cur &&p1 < p2)
			p2--;
		while (arr[p1] <= cur &&p1 < p2)
			p1++;
		if (p1 < p2) {
			int temp = arr[p1];
			arr[p1] = arr[p2];
			arr[p2] = temp;
		}
	}
	arr[L] = arr[p1];
	arr[p1] = cur;
	sort6(arr, L, p1 - 1);
	sort6(arr, p1 + 1, R);

}

7.堆排序

  • 利用完全二叉树的特点，构造大根堆，然后首位元素交换

  • 父节点：（i - 1）/ 2 （节点从0开始）
  • 左孩子：i*2 + 1
  • 右孩子：i*2 + 2
    时间复杂度O(n * logN)、空间O(1)

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
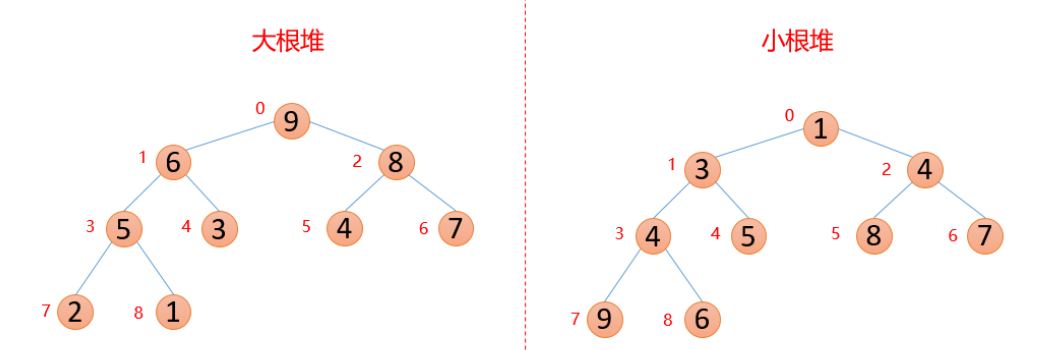
//堆是完全二叉树，满的二叉树，构造成大根堆，然后将上方最大的数和子节点交换
//一个节点的：父节点--(i-1) /2
//            父节点-- i*2 + 1
//            父节点-- i*2 + 2
//将数组构造成大根堆，然后以此往复

void heapSort(vector<int>&arr, int len) {
	for (int i = 0; i < len; i++) {
		//father需要是最大节点
		int index = i;
		int fatherindex = (index - 1) / 2;

		while (arr[index] > arr[fatherindex]) {
			int temp = arr[index];
			arr[index] = arr[fatherindex];
			arr[fatherindex] = temp;

			//index重新赋值
			index = fatherindex;
			fatherindex = (index - 1) / 2;
		}
	}
};
void sort7(vector<int>&arr)
{
	int len = arr.size();
	for (int i = len; i > 0; i--) {
		heapSort(arr, i);

		//交换元素
		int temp = arr[0];
		arr[0] = arr[i - 1];
		arr[i - 1] = temp;
	}
}

STL_优先队列

  • 1.快排

  • 2.堆排序

  • 快排

  • 数组中第K大的数（无序数组）

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    int findKthLargest(vector<int>& nums, int k) {
    	int len = nums.size();
    	return quickSort(nums, 0, len - 1, len - k);
    }
    int quickSort(vector<int>& nums, int left, int right, int k) {
    	int len1 = left;
    	int len2 = right;

    	int base = nums[left];
    	while (len1 < len2) {
    		while (nums[len2] >= base && len1 < len2)
    			len2--;
    		while (nums[len1] <= base && len1 < len2)
    			len1++;
    		if (len1 < len2) {
    			int temp = nums[len1];
    			nums[len1] = nums[len2];
    			nums[len2] = temp;
    		}
    	}
    	//握手,元素换位
    	nums[left] = nums[len1];
    	nums[len1] = base;

    	if (k == len1)
    		return nums[len1];
    	else if (k < len1)
    		return quickSort(nums, left, len1 - 1, k);
    	else
    		return quickSort(nums, len1 + 1, right, k);
    }

优先队列

  • 堆排序：（剑指_41）

  • #include
  • priority_queue<int, vector, std::less> maxStack;//大顶堆—返回最大元素
  • priority_queue<int, vector, std::greater> minStack;//小顶堆—返回最小元素

img

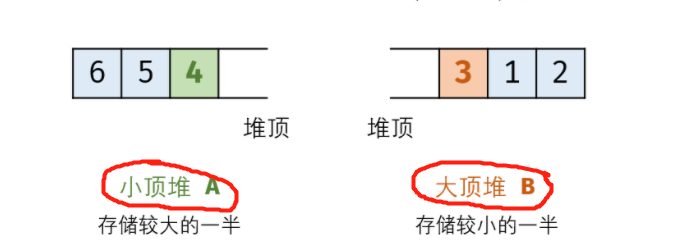
  • 题目：数组中第K大的数

  • 维护一个小顶堆即可

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    int findKthLargest(vector<int> &nums, int k)
    {
    	int result = 0;
    	int numsSize = int(nums.size());
    	if (numsSize == 0 || k > numsSize)
    	{
    		return 0;
    	}

    	priority_queue<int, vector<int>, greater<int>> store;
    	//堆中维持k个最大数
    	for (int i = 0; i < numsSize; i++)
    	{
    		store.push(nums[i]);
    		if (int(store.size()) > k)
    		{
    			store.pop();
    		}
    	}

    	result = store.top();
    	return result;
    }

二分查找库函数

  • 头文件：algorithm

  • lower_bound( begin,end,num )

    • 查找第一个大于或等于num的数字—— >= num

  • upper_bound( begin,end,num )

    • 查找第一个大于num的数字 —— > num

  • 例题LeetCode870：给定两个大小相等的数组 A 和 B，A 相对于 B 的优势可以用满足 A[i] > B[i] 的索引 i 的数目来描述。

  • 返回 A 的任意排列，使其相对于 B 的优势最大化。

  • 输入：A = [2,7,11,15], B = [1,10,4,11]

  • 输出：[2,11,7,15]

  • 输入：A = [12,24,8,32], B = [13,25,32,11]

  • 输出：[24,32,8,12]

  • 解题方法：田忌赛马

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    vector<int> advantageCount(vector<int>& A, vector<int>& B) {
    	sort(A.begin(), A.end());
    	vector<int> ans;
    	for (int i = 0; i < B.size(); i++) {
    		auto iter = upper_bound(A.begin(), A.end(), B[i]);
    		if (iter != A.end()) {
    			ans.push_back(*iter);
    			A.erase(iter);
    		}
    		else {
    			ans.push_back(A[0]);
    			A.erase(A.begin());
    		}
    	}
    	return ans;
    }

非比较类排序

8.计数

  • 1-100最快的排数，适用于数字范围不大地数字段。

    • 1.找到数组最大值和最小值
    • 2.count_arr[arr[i] ]++
    • 3.依次将数组填入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//8.计数排序，输入的数据值转化为键值存在于新开辟的数组空间中
void sort8(vector<int>&arr) {
	int max = 0;
	int min = 0;

	for (int i = 0; i < arr.size(); i++) {
		if (arr[i] > max)
			max = arr[i];
		if (arr[i] < min)
			min = arr[i];
	}
	vector<int>count(max + 1, 0);//辅助数组1--存放元素出现统计次数
	vector<int>tmp(arr);         //辅助数组2--原数组

	for (auto it : arr) {        //记录下标
		count[it]++;
	}
	for (int i = 1; i <= max; i++) {   //记录当前元素比他大数的数量
		count[i] = count[i] + count[i - 1];
	}
	for (int i = arr.size() - 1; i >= 0; i--) {
		arr[count[tmp[i]]-1] = tmp[i];
		//tmp[i] 数组的一个数，count[ tmp[i] ]大于这个数出现的次数 
		//arr[count[tmp[i]]]  相应的位置就应该是那个数  tmp[i]
		count[tmp[i]]--;
	}
}

9.基数

  • 按照个位、十位、百位依次顺序排序。

    1
    int minimumTotal(vector<vector<int>>& triangle) {

10.桶排序

  • 1.首先对元素进行分组 2.组内元素快速排序 3.依次将元素填充

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    //9.桶排序
    void sort9(vector<int>&arr){
    	int max = 0;
    	for (int i = 0; i < arr.size(); i++) {
    		if (arr[i] > max)
    			max = arr[i];
    	}
    	
    	int count = 0;
    	vector<int>temp(max + 1, 0);
    	for(int i = 0; i < arr.size(); i++) {
    		temp[arr[i]]++;
    	}
    	for(int i = 0; i <= max; i++) {
    		if (temp[i] > 0) {
    			for(int j = 0; j < temp[i]; j++) {
    				arr[count] = i;
    				count++;
    			}
    		}
    	}

    }

Top_K问题

第K大的数

  • 快排思想
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int findKth(vector<int> a, int n, int K) {
	// write code here
	//第1大   N-1
	//第2大   N-2
	//第K大   N-K
	return sortsort(a, n - K, 0, n - 1);
}
//利用快排来实现
int sortsort(vector<int>a, int K, int L, int R) {
	int cur = a[L];
	int p1 = L;
	int p2 = R;
	while (p1 < p2) {
		while (p1 < p2 && a[p2] >= cur)
			p2--;
		while (p1 < p2 && a[p1] <= cur)
			p1++;
		if (p1 < p2)
			swap(a[p1], a[p2]);
	}
	a[L] = a[p1];
	a[p1] = cur;
	if (p1 == K)
		return a[p1];
	else if (p1 < K)
		return sortsort(a, K, p1 + 1, R);
	else
		return sortsort(a, K, L, p1 - 1);
}

第K大的前K个数

  • 1.排序
  • 2.构造大根堆
  • 3.快排 + 二分
1
2


文章作者: Inter
文章链接: https://zuizichuan.cn/2020/07/29/LeetCode-%E5%8D%81%E5%A4%A7%E6%8E%92%E5%BA%8F-1/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Zichuan365' Blog！