Zichuan365' Blog HomeArchivesCategoriesGalleryAbout
LeetCode / 其他算法
|LeetCode其他算法

快慢指针

访问链表中倒数第K个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
ListNode* removeNthFromEnd(ListNode* head, int n) {
	// write code here
	ListNode* fast = head;
	ListNode* slow = head;
	while (n--) {
		if (fast)
			fast = fast->next;
		else
			return NULL;
	}

	while (fast) {
		fast = fast->next;
		slow = slow->next;
	}
	return slow;
}

删除链表中倒数第K个数

  • 快指针先走k，然后快慢同时走，快==NULL，到达目的地。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
ListNode* removeNthFromEnd(ListNode* head, int n) {
	// write code here
	ListNode* fast = head;
	ListNode* slow = head;
	while (n--) {
		if (fast)
			fast = fast->next;
		else
			return NULL;
	}
	//删除最后一个节点
	if (fast == NULL)
		return head->next;

	//删除所以这里是fast->next，返回的话这里是fast
	while (fast->next) {
		fast = fast->next;
		slow = slow->next;
	}
	slow->next = slow->next->next;
	return head;
}

2.环形链表的判断（leetcode_141）

  • 当存在环形链表，快指针肯定能够追上慢指针，此时return true;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool hasCycle(ListNode *head) {
	if (head == NULL || head->next == NULL)  return false;

	ListNode* fast = head;
	ListNode* slow = head;

	while (fast->next != NULL && fast->next->next != NULL) {
		fast = fast->next->next;
		slow = slow->next;
		if (fast == slow)
			return true;
	}
	return false;
}

3.环形链表的入口（leetcode_142）

img

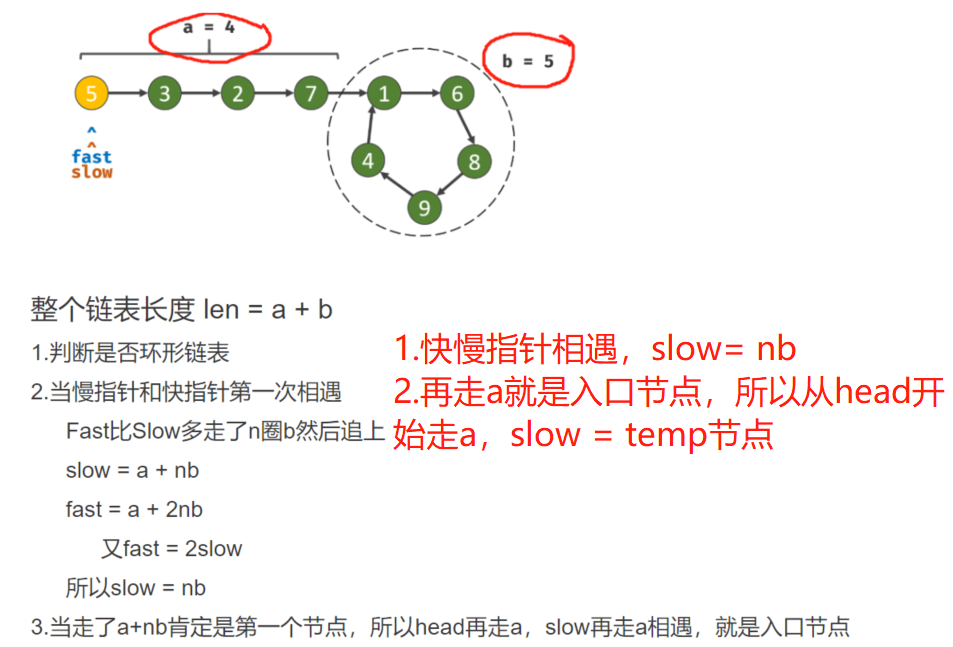
  1. slow和fast相遇，slow = nb
  2. slow再走a就能到达入口节点，所以当slow = temp就是入口节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
ListNode *detectCycle(ListNode *head) {
	bool flag = false;
	//判断是否为环形链表
	if (head == NULL || head->next == NULL)  return NULL;
	ListNode* fast = head;
	ListNode* slow = head;
	while (fast->next != NULL && fast->next->next != NULL) {
		fast = fast->next->next;
		slow = slow->next;
		if (fast == slow) {
			flag = true;
			break;
		}
	}
	if (flag) {
		ListNode* q = head;
		while (q != slow)
		{
			q = q->next;
			slow = slow->next;
		}
		return q;
	}
	return NULL;
}

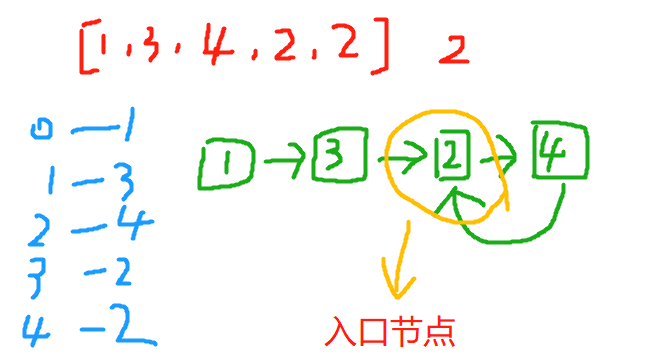
4. 寻找重复数（leetcode_287）

  • 给定一个包含 n + 1 个整数的数组 nums，其数字都在 1 到 n 之间（包括 1 和 n），可知至少存在一个重复的整数。假设只有一个重复的整数，找出这个重复的数。

  • 输入: [1,3,4,2,2]

  • 输出: 2

  • 输入: [3,1,3,4,2]

  • 输出: 3

  • 解：运用环形链表来求解问题
    img

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    int findDuplicate(vector<int>& nums) {
    	int fast = 0, slow = 0;

    	while (1) {
    		//根据索引自动成环
    		slow = nums[slow];
    		fast = nums[fast];
    		fast = nums[fast];
    		// 快指针index = 慢指针index
    		if (slow == fast) {
    			int begin = 0;//头节点从0开始走,慢指针走,两者再相等，就是入环的第一个index
    			while (nums[slow] != nums[begin]) {
    				begin = nums[begin];
    				slow = nums[slow];
    			}
    			return nums[slow];
    		}
    	}
    }

5.链表的中间结点（leetcode_876）

1
2
3
4
5
6
7
8
9
10
11
12
13
ListNode* middleNode(ListNode* head) {
	if (head == NULL || head->next == NULL)
		return head;

	ListNode* fast = head;
	ListNode* slow = head;
	while (fast != NULL && fast->next != NULL) {
		fast = fast->next->next;
		slow = slow->next;
	}

	return slow;
}

6.快乐数（leetcode_202）

  • 输入：19

  • 输出：true

  • 解释：

  • 1^2 + 9^2 = 82

  • 8^2 + 2^2 = 68

  • 6^2 + 8^2 = 100

  • 1^2 + 0^2 + 0^2 = 1

  • 接下来再进行计算，就一直是1了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//求取一个数的Sum, 19 / 1^2 + 9^2 = 82 
int cal(int n) {
	int sum = 0;
	while (n > 0) {
		int bit = n % 10;
		sum += bit * bit;
		n = n / 10;
	}
	return sum;
}

bool isHappy(int n) {
	int slow = n, fast = n;
	//do_while和while的区别,先进行一次再判断while
	
   //快乐数无循环，fast追上slow，判断其是不是1，如果不是则是无限循环。 
   slow = cal(slow);
	fast = cal(fast);
	fast = cal(fast);
	while (slow != fast) {
		slow = cal(slow);
		fast = cal(fast);
		fast = cal(fast);
	}
	return slow == 1? true:false;
}

欧几里得算法（辗转相除法）

  • 求取最大公约数

  • 输入：（a >= b）
  • 具体算法：gcd（a，b）=gcd（b，a%b）
    1
    2
    3
    int gcd(int a,int b){
    	return b==0?a:gcd(b,a%b);
    }

字符串的最大公因子(leetcode_1071)

img

  • 解

1
2
3
4
5
6
7
8
9
10
int gcd(int a, int b) {
	return b == 0 ? a : gcd(b, a%b);
}

string gcdOfStrings(string str1, string str2) {
	if (str1 + str2 != str2 + str1)
		return "";
	return str1.substr(0, gcd(str1.size(), str2.size()));

}

水壶倒水问题(leetcode_365)

  • 有两个容量分别为 x升 和 y升 的水壶以及无限多的水。请判断能否通过使用这两个水壶，从而可以得到恰好 z升 的水？

  • 如果可以，最后请用以上水壶中的一或两个来盛放取得的 z升水。

  • 你允许：

  • 1.装满任意一个水壶

  • 2.清空任意一个水壶

  • 3.从一个水壶向另外一个水壶倒水，直到装满或者倒空

  • 原理是ax+by=z 求二元一次方程的整数解 有整数解的前提是 x与y的最大公约数 能被z整除

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    int gcd(int a, int b) {
    	return b == 0 ? a : gcd(b, a%b);
    }
    bool canMeasureWater(int x, int y, int z) {
    	if (x + y < z)
    		return false;
    	if (x == z || y == z || x + y == z || z == 0)
    		return true;
    	return z % gcd(x, y) == 0;
    }

约瑟夫环问题

剑指Offer 62. 圆圈中最后剩下的数字

  • 0,1,,n-1这n个数字排成一个圆圈，从数字0开始，每次从这个圆圈里删除第m个数字。求出这个圆圈里剩下的最后一个数字。

  • 例如，0、1、2、3、4这5个数字组成一个圆圈，从数字0开始每次删除第3个数字，则删除的前4个数字依次是2、0、4、1，因此最后剩下的数字是3。

  • 输出

  • 输入: n = 5, m = 3

  • 输出: 3

  • 输入: n = 10, m = 17

  • 输出: 2

  • 方法：约瑟夫环问题
    img
    img

1
2
3
4
5
6
7
8
int lastRemaining(int n, int m) {
	//约瑟夫环的问题
	int res = 0;
	for (int i = 2; i <= n ; i++) {
		res = (res + m) % i;
	}
	return res;
}

中心扩展法(回文串相关)

  • 求取最长回文串

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    //中心扩展发
    string longestPalindrome(string s) {

    	if (s.size() <= 1)
    		return s;

    	int L = 0;
    	int R = 0;
    	//记录当前最大回文串地址下标
    	int len = 1;
    	for (int i = 0; i < s.size(); i++) {
    		int len1 = calcuNum(s, i, i);
    		int len2 = calcuNum(s, i, i + 1);

    		int lentemp = max(len1, len2);

    		//当当前回文子串大于之前的，统计当前下标
    		if (lentemp > len) {
    			L = i - (lentemp - 1) / 2;
    			//R = i + lentemp / 2; 
    			len = lentemp;
    		}
    	}
    	return s.substr(L, len);
    }
    //从这点出发的回文子串
    int calcuNum(string s, int L, int R) {
    	while (L >= 0 && R < s.size() && s[L] == s[R]) {
    		L--;
    		R++;
    	}
    	return  R - L - 1;
    }

  • 头部加入最少字符，变成回文串

  • 尾部加入最少字符，变成回文串
    img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
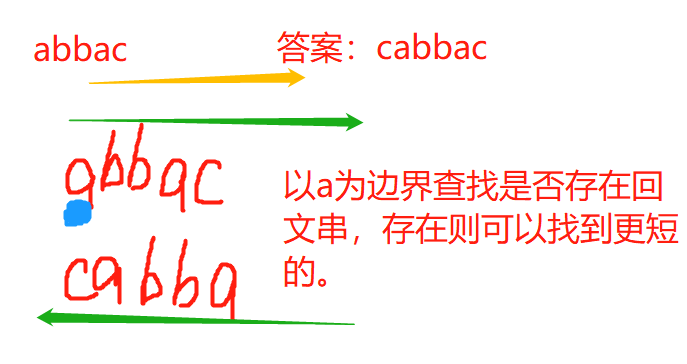
//头部加入字符，变成回文串
//解题：
//找寻以头节点为中心，是否存在回文串
string shortestPalindrome(string s)
{
	string rev(s);
	reverse(rev.begin(), rev.end());

	int len = s.size();
	for (int i = 0; i < len; i++) {
		if (s.substr(0 , len - i) == rev.substr(i)) {
			return rev.substr(0 , i) + s;
		}
	}
	return "";
}
//尾部加入字符，变成回文串
//解题：
//找寻以尾节点为中心，是否存在回文串
string shortestPalindromePop(string s)
{
	string rev(s);
	reverse(rev.begin(), rev.end());

	int len = s.size();
	for (int i = 0; i < len; i++) {
		if (s.substr(i) == rev.substr(0,len - i)) {
			return s + rev.substr(len - i);
		}
	}
	return "";
}

前缀和Sum_K

数组的连续子集，Sum的可能性

  1. unordered_map<int, int>dp;
  2. sum += arr[i]
  3. 对sum处理
  4. res += dp[sum]
  5. dp[sum]++

1.求取和为 K 的连续子数组(leetcode_560)

  • 给定一个整数数组和一个整数 k，你需要找到该数组中和为 k 的连续的子数组的个数。

  • 输入：[1,1,1] \ k=2

  • 输出：[1,1]、[1,1]

  • 思路：SumK的方法，利用哈希表来快速统计Sum是否出现过，然后进行对应计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int subarraySum(vector<int>& nums, int k)
{
	//Sum  K
	unordered_map<int, int>vis;
	int sum = 0;
	int res = 0;
	vis[0] = 1;
	for (int i = 0; i < nums.size(); i++) {
		sum += nums[i];
		res += vis[sum - k];
		vis[sum]++;
	}
	return res;
}

2.和可被 K 整除的子数组(leetcode_974)

  • 给定一个整数数组 A，返回其中元素之和可被 K 整除的（连续、非空）子数组的数目。

  • 输入：A = [4,5,0,-2,-3,1], K = 5

  • 输出：7

  • 解释：

  • 有 7 个子数组满足其元素之和可被 K = 5 整除：

  • [4, 5, 0, -2, -3, 1], [5], [5, 0], [5, 0, -2, -3], [0], [0, -2, -3], [-2, -3]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int subarraysDivByK(vector<int>& A, int K) {
	unordered_map<int, int>vis;
	vis[0] = 1;//余数为0，空直接满足就是1
	int res = 0;
	int sum = 0;
	for (int i = 0; i < A.size(); i++) {
		sum += A[i];

//加上偏移量
//在C++中负数取余仍然是负数，所以我们要将这个取余后的负数加上K，就变成正数，与其他状态进行合并。
//比如k=5, -6%5= -1,他的状态的等于4的,我们加上一个偏移量k,便于计算
//-1+1%5=0,-1+6%5=0

		if (sum%K < 0)  //当K = 5,-2和2满足要求，所以我都将负数转换为正数来方便计算
			sum = sum % K + K;
		else
			sum = sum % K;

		res += vis[sum];//相同余数的情况
		vis[sum]++;//余数情况添加
	}
	return res;
}

3.判断是否存在Sum为 K 的连续子数组(leetcode_523)

  • 给定一个包含 非负数 的数组和一个目标 整数 k，编写一个函数来判断该数组是否含有连续的子数组，其大小至少为 2，且总和为 k 的倍数，即总和为 n*k，其中 n 也是一个整数。

  • 输入：[23,2,4,6,7], k = 6

  • 输出：True

  • 解释：[2,4] 是一个大小为 2 的子数组，并且和为 6。

  • 输入：[23,2,6,4,7], k = 6

  • 输出：True

  • 解释：[23,2,6,4,7]是大小为 5 的子数组，并且和为 42。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
bool checkSubarraySum(vector<int>& nums, int k) {
	int sum = 0;
	//map<sum % K,下标>
	unordered_map<int, int> map;
	//sum==0的下标为-1,第一个元素的i是0,所以为了保证大小至少为2,map[0] = -1。
	map[0] = -1;
	for (int i = 0; i < nums.size(); i++) {
		sum += nums[i];
		if (k != 0)
			sum = sum % k;

		//没找到下标
		if (map.find(sum) == map.end())
			map[sum] = i;
		else { //找到下标
			if (i - map[sum] > 1)//其大小至少为2     
				return true;
		}
	}
	return false;
}

筛漏法（找素数）

计数质数(leetcode204)

  • 1不是素数

  • 统计所有小于非负整数 n 的质数的数量。

  • 输入: 10

  • 输出: 4

  • 解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    int countPrimes(int n) {
    	vector<bool> vis(n, true);
    	int cnt = 0;

    	for (int i = 2; i < vis.size(); i++) {
    		if (vis[i]) {
    			cnt++;
    			//筛漏法,将2的乘数全部筛除
    			for (int j = 2; j*i < vis.size(); j++)
    				vis[j*i] = false;
    		}
    	}
    	return cnt;
    }
文章作者: Inter
文章链接: https://zuizichuan.cn/2020/07/30/LeetCode-%E5%85%B6%E4%BB%96%E7%AE%97%E6%B3%95/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Zichuan365' Blog！