LeetCode / 滑动窗口 | Zichuan365' Blog

56.合并区间（重要）

给出一个区间的集合，请合并所有重叠的区间。
输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]

解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

vector<vector<int>> merge(vector<vector<int>>& arr) {
	if (arr.size() <= 1)
		return arr;
	//排序
	sort(arr.begin(), arr.end());
	vector<vector<int>>res;
	int len = arr.size();
	int L = 0;
	int R = 0;
	while (R < len) {
		if (arr[L][1] >= arr[R][1]) {
			R++;
			}
		else if (arr[L][1] < arr[R][0]){
			res.push_back(arr[L]);
			L = R;
		}
		else {
			arr[L][1] = arr[R][1];
			R++;
		}
	}
	res.push_back(arr[L]);//添加最后元素
	return res;
}

滑动窗口问题

求解的是连续子集问题

优秀博文：https://blog.csdn.net/qq_43152052/article/details/102840715
①窗口由两个指针构成，一个左指针left，一个右指针right，然后[left,right]表示的索引范围是一个窗口了。
②右指针right的功能是用来扩展窗口：当窗口内的条件没有达到题目要求时，我们需要不断移动右指针right直到窗口内的条件第一次满足题目要求为止。
③左指针left的功能是用来缩小窗口的：当窗口内的条件已满足题目条件或多于题目条件时（窗口溢出），我们缩小窗口，也就是左指针left需要右移直到窗口条件不满足为止。这时，我们需要记录当前窗口的大小，并更新目前为止满足条件的最小窗口记录。之后，再次扩展右指针right，使得窗口满足题目的条件。

固定套路

int left = 0，res = 0;
int tiaojian = 0;
//满足情况：扩大右指针
//不满足情况：移动左值针，缩小范围
for(int i = 0;i<arr.size();i++){

}

424.替换后的最长重复字符

给你一个仅由大写英文字母组成的字符串，你可以将任意位置上的字符替换成另外的字符，总共可最多替换 k 次。在执行上述操作后，找到包含重复字母的最长子串的长度。
输入:
s = “ABAB”, k = 2
输出:
4
输入:
s = “AABABBA”, k = 1
输出:
4
解题：

滑动窗口范围内的数字替换成区间内数最多的数
所以定义变量maxNum为当前区间数量最多的那个数
当不满足情况的时候，左值针移动，利用辅助数组vectorABC(26,0);

int characterReplacement(string s, int k) {

	vector<int>vis(26, 0);
	int left = 0, res = 0, numSize = 0;
	//numSize当前窗口中数量最多的数    
	for (int i = 0; i < s.size(); i++) {
		vis[s[i] - 'A']++;
		numSize = max(vis[s[i] - 'A'], numSize);
		//i - left + 1当前区间所有元素数量
		while (i - left + 1 - numSize > k) {
			vis[s[left] - 'A']--;
			left++;
		}
		res = max(res, i - left + 1);
	}
	return res;

}

3. 无重复字符的最长子串

给定一个字符串，请你找出其中不含有重复字符的最长子串的长度。
输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
输入: “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
解题：只有可能是新添加进来的那个数字，出现重复数字。

int lengthOfLongestSubstring(string s) {

	vector<int>vis(256, 0);
	int left = 0, res = 0;

	for (int i = 0; i < s.size(); i++) {
		vis[s[i]]++;
		while (vis[s[i]] > 1) {
			vis[s[left]]--;
			left++;
		}
		res = max(res, i - left + 1);
	}
	return res;
}

76. 最小覆盖子串(困难)

给你一个字符串 S、一个字符串 T 。请你设计一种算法，可以在 O(n) 的时间复杂度内，从字符串 S 里面找出：包含 T 所有字符的最小子串。
输入：S = “ADOBECODEBANC”, T = “ABC”
输出：”BANC”
解题：滑动窗口
需要判断的主要是满不满足T中的字符数量，使用vectorvis,和match来双重判断
满足数量match++
当产生数量变化match–
只有当vis[i] == vis[need]才进行match++，保证了match不会出现大于其max的情况

#include <limits.h>

string minWindow(string s, string t) {
	int left = 0, len = INT_MAX, leftres = 0;
	string resString;

	vector<int>vis(256, 0);
	vector<int>need(256, 0);
	for (auto it : t)
		vis[it]++;

	int matchSuccess = 0;

	for (auto it : vis) {
		if (it != 0)
			matchSuccess++;
	}

	int match = 0;
	for (int i = 0; i < s.size(); i++) {
		char tempR = s[i];
		if (vis[tempR] > 0) {  //这个数是需要的
			need[tempR]++;
			if (need[tempR] == vis[tempR])
				match++;
		}

		while (match == matchSuccess) {
			char tempL = s[left];
			if (vis[tempL] <= 0)
				left++;
			else {
				need[tempL]--;
				left++;
				if (need[tempL] < vis[tempL]) {//match不匹配了需要恢复
					need[tempL]++;
					left--;
					break;
				}
			}
		}

		if (match == matchSuccess && i - left + 1 < len) {
			leftres = left;
			len = i - left + 1;
		}
	}
	return len == INT_MAX ? "" : s.substr(leftres, len);
}

239. 区间的滑动窗口最大值 / deque

给定一个数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
题目：
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 —– 最大值
[1 3 -1] -3 5 3 6 7 —– 3
1 [3 -1 -3] 5 3 6 7 —– 3
1 3 [-1 -3 5] 3 6 7 —– 5
1 3 -1 [-3 5 3] 6 7 —– 5
1 3 -1 -3 [5 3 6] 7 —– 6
1 3 -1 -3 5 [3 6 7] —– 7
解题：
利用双向队列的堆栈特性
pop_back()\ pop_front() \ push_back()\ push_front()\ A.front()\ A.back()
- 头部保存最大元素
- 利用存放元素下标来保证没有超出区间的范围
- 每次比较和尾部数据进行比较，从而保证前面节点：老元素。后面节点：新元素。这样可以完成上一条。

vector<int> maxSlidingWindow(vector<int>& nums, int k) {
	if (nums.size() == 0)
		return {};
	vector<int>res;
	deque<int>deque;

	//头部:最大数据
	//尾部比较，然后淘汰元素:保证了老元素前,新元素后
	//元素下标,保证区间范围
	for (int i = 0; i < nums.size(); i++) {
		if (!deque.empty() && i - deque.front() >= k)
			deque.pop_front();
		while (!deque.empty() && nums[i] > nums[deque.back()])
			deque.pop_back();
		//这里忘记了
		deque.push_back(i);
		//这里忘记了
		if (i - k + 1 >= 0)
			res.push_back(nums[deque.front()]);
	}
	return res;
}

438. 找到字符串中所有字母异位词（固定窗口）

固定窗口、两个:vectorA == vectorB即可
固定窗口、两个:vectorA == vectorB即可

vectorvis(256, 0);
vectorneed(256, 0);
need == vis

给定一个字符串 s 和一个非空字符串 p，找到 s 中所有是 p 的字母异位词的子串，返回这些子串的起始索引。
字符串只包含小写英文字母，并且字符串 s 和 p 的长度都不超过 20100。

题目：
输入: s: “cbaebabacd” p: “abc”
输出: [0, 6]
输入:s: “abab” p: “ab”
[0, 1, 2]
解题固定窗口，求是否满足

vector<int> findAnagrams(string s, string p) {

	if (p.size() > s.size())
		return{};

	//连续的子串
	vector<int>vis(256, 0);
	vector<int>need(256, 0);

	vector<int>res;
	for (auto it : p)
		vis[it]++;

	int left = 0;
	int H = p.size();
	//固定长度的滑动窗口
	for (int i = 0; i < s.size(); i++) {
		if (i < H) {
			need[s[i]]++;
			continue;
		}
		if (vis == need)
			res.push_back(left);

		need[s[i]]++;
		need[s[left++]]--;
	}
	if (vis == need)
		res.push_back(left);
	return res;
}

480. 滑动窗口中位数（困难—不会）

中位数是有序序列最中间的那个数。如果序列的大小是偶数，则没有最中间的数；此时中位数是最中间的两个数的平均数。
[2,3,4]，中位数是 3
[2,3]，中位数是 (2 + 3) / 2 = 2.5
给出 nums = [1,3,-1,-3,5,3,6,7]，以及 k = 3。

窗口位置中位数
[1 3 -1] -3 5 3 6 7 ———— 1
1 [3 -1 -3] 5 3 6 7 ———— -1
1 3 [-1 -3 5] 3 6 7 ———— -1
1 3 -1 [-3 5 3] 6 7 ———— 3
1 3 -1 -3 [5 3 6] 7 ———— 5
1 3 -1 -3 5 [3 6 7] ———— 6

vector<double> medianSlidingWindow(vector<int>& nums, int k) {
	int nums_size = nums.size();
	multiset<int> window(nums.begin(), nums.begin() + k);
	//mid即是high_p
	multiset<int>::iterator mid = window.begin();
	for (int i = 0; i < k / 2; ++i)
		++mid;
	vector<double> ans;
	ans.reserve(nums_size - k + 1);
	for (int i = k;; ++i)
	{
		if (k % 2 == 0)
		{
			multiset<int>::iterator low_p = prev(mid, 1);
			ans.push_back(((double)*low_p + *mid) / 2.0);
		}
		else
		{
			ans.push_back(*mid);
		}
		if (i == nums_size)
			break;
		window.insert(nums.at(i));
		if (nums.at(i) < *mid)
			--mid;
		if (nums.at(i - k) <= *mid)
			++mid;
		window.erase(window.find(nums.at(i - k)));
	}
	return ans;
}

567.字符串的排列（固定窗口—438一样）

给定两个字符串 s1 和 s2，写一个函数来判断 s2 是否包含 s1 的排列。
换句话说，第一个字符串的排列之一是第二个字符串的子串。
输入: s1 = “ab” s2 = “eidbaooo”
输出: True
解释: s2 包含 s1 的排列之一 (“ba”).
输入: s1= “ab” s2 = “eidboaoo”
输出: False

bool checkInclusion(string s1, string s2) {
	if (s1.size() > s2.size())
		return{};

	//连续的子串
	vector<int>vis(256, 0);
	vector<int>need(256, 0);

	for (auto it : s1)
		vis[it]++;

	int left = 0;
	int H = s1.size();
	//固定长度的滑动窗口
	for (int i = 0; i < s2.size(); i++) {
		if (i < H) {
			need[s2[i]]++;
			continue;
		}
		if (vis == need)
			return true;

		need[s2[i]]++;
		need[s2[left++]]--;
	}
	if (vis == need)
		return true;
	return false;
}

992. K个不同整数的子数组

给定一个正整数数组 A，如果 A 的某个子数组中不同整数的个数恰好为 K，则称 A 的这个连续、不一定独立的子数组为好子数组。
（例如，[1,2,3,1,2] 中有 3 个不同的整数：1，2，以及 3。）
返回 A 中好子数组的数目。
输入：A = [1,2,1,2,3], K = 2
输出：7
解释：恰好由 2 个不同整数组成的子数组：[1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].
输入：A = [1,2,1,3,4], K = 3
输出：3
解释：恰好由 3 个不同整数组成的子数组：[1,2,1,3], [2,1,3], [1,3,4].
采用unordered_map<int,int>来统计,

int subarraysWithKDistinct(vector<int>& A, int K) {
	if (K == 0 || A.empty())
		return 0;

	unordered_map<int, int>vis;
	int left = 0, res = 0;

	for (int i = 0; i < A.size(); i++) {
		vis[A[i]]++;

		while (vis.size() > K) {
			if (vis[A[left]] > 1)
				vis[A[left]]--;
			else
				vis.erase(A[left]);

			left++;
		}

		int tempL = left;//当前的左指针位置,然后右移看子集有没有满足要求的
		while (vis.size() == K) {
			res++;
			if (vis[A[left]] > 1)
				vis[A[left]]--;
			else
				vis.erase(A[left]);

			left++;
		}
		//还原
		while (left > tempL) {

			vis[A[left - 1]]++;
			left--;
		}
	}
	return res;
}

995. K 连续位的最小翻转次数（类似翻金币）（困难不会）

在仅包含 0 和 1 的数组 A 中，一次 K 位翻转包括选择一个长度为 K 的（连续）子数组，同时将子数组中的每个 0 更改为 1，而每个 1 更改为 0。
返回所需的 K 位翻转的次数，以便数组没有值为 0 的元素。如果不可能，返回 -1。
输入：A = [0,1,0], K = 1
输出：2
解释：先翻转 A[0]，然后翻转 A[2]。

输入：A = [1,1,0], K = 2
输出：-1
解释：无论我们怎样翻转大小为 2 的子数组，我们都不能使数组变为 [1,1,1]。
输入：A = [0,0,0,1,0,1,1,0], K = 3
输出：3
解释：
翻转 A[0],A[1],A[2]: A变成 [1,1,1,1,0,1,1,0]
翻转 A[4],A[5],A[6]: A变成 [1,1,1,1,1,0,0,0]
翻转 A[5],A[6],A[7]: A变成 [1,1,1,1,1,1,1,1]

利用队列

int minKBitFlips(vector<int>& A, int K) {
	if (A.empty())return -1;

	int result = 0, N = A.size();
	queue<int> window;//window用来存放被反转元素的下标，window的长度表示反转的次数

	for (int i = 0; i < N; ++i)
	{
		//当下标之间的距离大于k时，需要移除队头下标了
		while (!window.empty() && window.front() + K <= i)
			window.pop();

		//当前位置的1反转奇数次为0，需要反转；当前位置的0反转偶数次还是为0，还是需要反转
		if (A[i] == window.size() % 2)
		{
			if (i + K > N)return -1;
			window.push(i);
			result++;
		}
	}
	return result;
}

978. 最长湍流子数组

数组的形式是升降升降升，这种形式
输入：[9,4,2,10,7,8,8,1,9]
输出：5
解释：(A[1] > A[2] < A[3] > A[4] < A[5])
题解：compare前后数据——遍历一遍数组

static const int N = 4e4 + 5;

// dp[i][0]表示以第i个元素结尾且是 下降 的最长的长度
// dp[i][1]表示以第i个元素结尾且是 上升 的最长的长度
int maxTurbulenceSize(vector<int>& A) {
	int n = A.size();

	int dp[N][2];
	dp[0][0] = dp[0][1] = 1;
	int res = 1;

	for (int i = 1; i < n; ++i) {
		dp[i][0] = dp[i][1] = 1;
		if (A[i] > A[i - 1])
			dp[i][1] = dp[i - 1][0] + 1;
		else if (A[i] < A[i - 1])
			dp[i][0] = dp[i - 1][1] + 1;


		res = max(res, max(dp[i][0], dp[i][1]));
	}
	return res;
}

https://blog.csdn.net/qq_43152052/article/details/102840715
1040.移动石子直到连续Ⅱ

1052.爱生气的书店老板

1074.元素和为目标值的子矩阵数量

1208.尽可能使字符串相等

11.盛最多的水

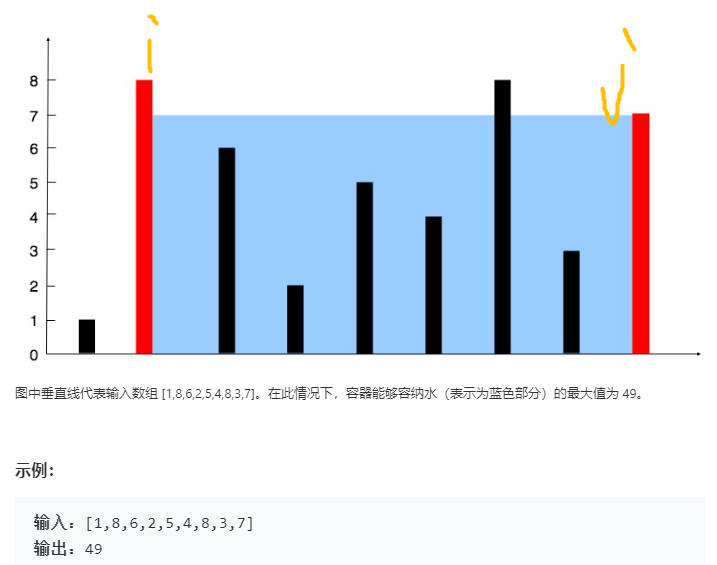
int maxArea(vector<int>& height) {
	int len = height.size();
	int L = 0;
	int R = len - 1;
	//消状态这点讲的很好，其实质就是在移动的过程中不断消去不可能成为最大值的状态。！
	//当 i = j 都只能减小，所以随便往哪边动都是减小
	//i > j,移动只能减小或者不变，所以移动j可能增加面积
	//尽可能的去增加面积
	int res = 0;
	while (L < R) {
		int h = min(height[L], height[R]);
		res = max(h *(R - L), res);
		if (height[L] >= height[R])
			R--;
		else
			L++;
	}
	return res;
}

腾讯面试题

https://www.nowcoder.com/discuss/488619
题目：
小Q在进行射击气球的游戏，如果小Q在连续T枪中打爆了所有颜色的气球，将得到一只QQ公仔作为奖励。（每种颜色的气球至少被打爆一只）。这个游戏中有m种不同颜色的气球，编号1到m。小Q一共有n发子弹，然后连续开了n枪。小Q想知道在这n枪中，打爆所有颜色的气球最少用了连续几枪？
输入描述：一个整数表示小Q打爆所有颜色气球用的最少枪数。如果小Q无法在这n枪打爆所有颜色的气球，则输出-1
例子：
输入：
12 5
2 5 3 1 3 2 4 1 0 5 4 3
输出：
6
解题：
1.暴力O(n^2)
2.滑动窗口O(n^2)

#include <iostream>
#include <vector>
#include <sstream>
#include <algorithm>

using namespace std;

int main() {
	//输入12 和 5
	int index = 3;
	vector<int>arr{ 0,3,3,3,3,2,1,2,3,2,2,3,1,2,3,2,2,1,0,0,0,0,0 };

	int res = 9999;
	int left = 0;
	int cnt = 0;
	vector<int>vis(index + 1, 0);
	for (int i = 0; i < arr.size(); i++) {
		vis[arr[i]]++;
		if (vis[arr[i]] == 1) {
			cnt++;
		}
		//cout << "i:"<<i << endl;
		//cout << "cnt:" << cnt << endl;

		if(cnt == vis.size()) {
			while (cnt == vis.size()) {
				int numtemp = arr[left];
				vis[numtemp]--;
				left++;
				
				if (vis[numtemp] == 0)
					cnt--;

			}
			left--;
			vis[arr[left]]++;
			cnt++;
			res = min(res, i - left + 1);
		}

	}
	cout << res;
	system("pause");
	return 0;
}

15.三数之和

给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。
注意：答案中不可以包含重复的三元组。
给定数组 nums = [-1, 0, 1, 2, -1, -4]，
满足要求的三元组集合为：
[
[-1, 0, 1],
[-1, -1, 2]

]

vector<vector<int>> threeSum(vector<int>& nums) {
	int len = nums.size();
	vector<vector<int>>res;
	sort(nums.begin(), nums.end());

	for (int i = 0; i < len - 2; i++) {
		int cur = nums[i];
		//大剪枝
		if (cur > 0) break;                     //最小的数大于0,不存在直接跳出
		//大剪枝
		if (i > 0 && cur == nums[i - 1])continue; //比如-2,-2,-1  :-2已经考虑了一个-2和两个-2
		int L = i + 1;
		int R = len - 1;
		// i、L 、R
		while (L < R) {
			if (nums[L] + nums[R] + cur > 0)R--;
			else if (nums[L] + nums[R] + cur < 0)L++;
			else {
				res.push_back({ cur,nums[L],nums[R] });
				L++;
				R--;
				//小剪枝
				while (L < R && nums[L] == nums[L - 1])L++;
				while (L < R && nums[R] == nums[R + 1])R--;//去除重复的元素
			}

		}
	}
	return res;
}

16.最接近的三数之和

给定一个包括 n 个整数的数组 nums 和一个目标值 target。找出 nums 中的三个整数，使得它们的和与 target 最接近。返回这三个数的和。假定每组输入只存在唯一答案。

输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。

int threeSumClosest(vector<int>& nums, int target) {
	sort(nums.begin(), nums.end());
	int res = nums[0] + nums[1] + nums[2];
	for (int i = 0; i < nums.size() - 2; i++) {
		int L = i + 1;
		int R = nums.size() - 1;
		while (L < R) {
			int resSum = nums[i] + nums[L] + nums[R];
			if (abs(target - resSum) < abs(target - res))
				res = resSum;

			if (resSum > target)
				R--;
			else if (resSum < target)
				L++;
			else
				return target;
		}
	}
	return res;
}

26.删除排序数组中的重复项

给定一个排序数组，你需要在原地删除重复出现的元素，使得每个元素只出现一次，返回移除后数组的新长度。
不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。
输入：给定数组 nums = [1,1,2]
输出：[1,2],2
输入：给定数组 nums = [0,0,1,1,1,2,2,3,3,4]

输出：[0,1,2,3,4],5

int removeDuplicates(vector<int>& nums) {
	if (nums.size() <= 1)
		return nums.size();

	int index = 0;
	for (int i = 1; i < nums.size(); i++) {
		//如果不相等,元素进行赋值,然后++
		if (nums[i] != nums[index]) {
			index++;
			nums[index] = nums[i];
		}
	}
	return index + 1;
}

209.长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。
输入：s = 7, nums = [2,3,1,2,4,3]
输出：2

解释：子数组 [4,3] 是该条件下的长度最小的子数组。

int minSubArrayLen(int s, vector<int>& nums) {
	//最大最小连续子数组,双指针滑动窗口
	int sum = 0;
	int len = 0;

	int left = 0;
	for (int i = 0; i < nums.size(); i++) {
		sum += nums[i];
		//找到>=s的最小连续数组，
		//所以当其>=s时计算结果,将其处理成<s
		while (sum >= s) {
			if (len == 0)
				len = i - left + 1;
			else
				len = min(len, i - left + 1);
			sum -= nums[left++];
		}
	}
	return len;
}

56.合并区间（重要）

滑动窗口问题

424.替换后的最长重复字符

3. 无重复字符的最长子串

76. 最小覆盖子串(困难)

239. 区间的滑动窗口最大值 / deque

438. 找到字符串中所有字母异位词（固定窗口）

480. 滑动窗口中位数（困难—不会）

567.字符串的排列（固定窗口—438一样）

992. K个不同整数的子数组

995. K 连续位的最小翻转次数（类似翻金币）（困难不会）

978. 最长湍流子数组

1040.移动石子直到连续Ⅱ

1052.爱生气的书店老板

1074.元素和为目标值的子矩阵数量

1208.尽可能使字符串相等

11.盛最多的水

腾讯面试题

15.三数之和

16.最接近的三数之和

26.删除排序数组中的重复项

209.长度最小的子数组