Zichuan365' Blog HomeArchivesCategoriesGalleryAbout
LeetCode / 回溯法
|LeetCode回溯法

回溯法

求解所有可能性问题的方法

  • 解决一个回溯问题，实际上就是一个决策树的遍历过程。

    • 1、结束条件：也就是到达决策树底层，无法再做选择的条件。return
    • 2、选择列表：也就是你当前可以做的选择。
    • 3、路径：也就是已经做出的选择。
      img1
      img1

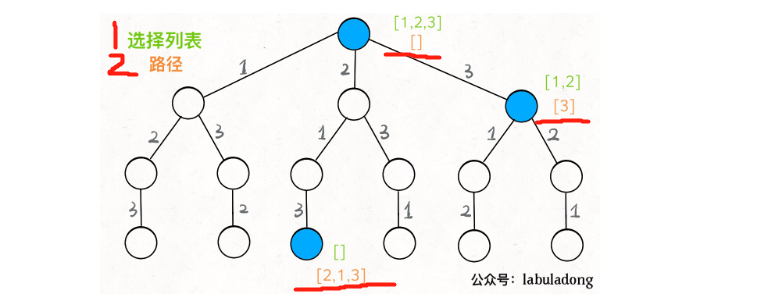
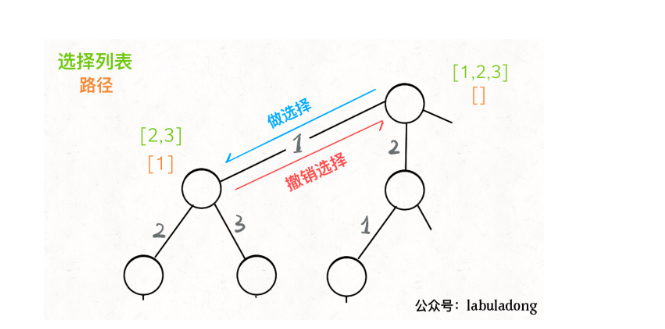
固定套路

  • 1、结束条件
  • 2、条件选择
  • 3、做出选择
  • 4、继续dfs
  • 5、撤销选择

全排列问题——————

123、132———————

46.全排列（无重复、最经典）

  • 给定一个 没有重复 数字的序列，返回其所有可能的全排列。

  • 输入: [1,2,3]

  • 输出:

  • [

  • [1,2,3],

  • [1,3,2],

  • [2,1,3],

  • [2,3,1],

  • [3,1,2],

  • [3,2,1]

  • ]

  • 解题：最经典的回溯法求问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
vector<vector<int>>res;
vector<vector<int>> calculate(vector<int>& nums) {
	vector<int>arr;
	//辅助判断函数
   vector<bool>vis(nums.size(), false);
	dfs(nums, arr, vis);
	return res;
}

void dfs(vector<int>& nums, vector<int>& arr, vector<bool>& vis) {
	//结束条件
	if (arr.size() == nums.size()) {
		res.emplace_back(arr);
		return;
	}
	for (int i = 0; i < nums.size(); i++) {
		//条件选择
		if (vis[i])continue;
		
		//做出选择
		arr.emplace_back(nums[i]);
		vis[i] = true;
		
		//继续dfs
		dfs(nums, arr, vis);
		
		//撤销选择
		arr.pop_back();
		vis[i] = false;
	}
}

47.全排列II（重复元素，unordered_map存储元素）

  • 给定一个可包含重复数字的序列，返回所有不重复的全排列。

  • 输入: [1,1,2]
  • 输出:
  • [
  • [1,1,2],
  • [1,2,1],
  • [2,1,1]
  • ]
    img1

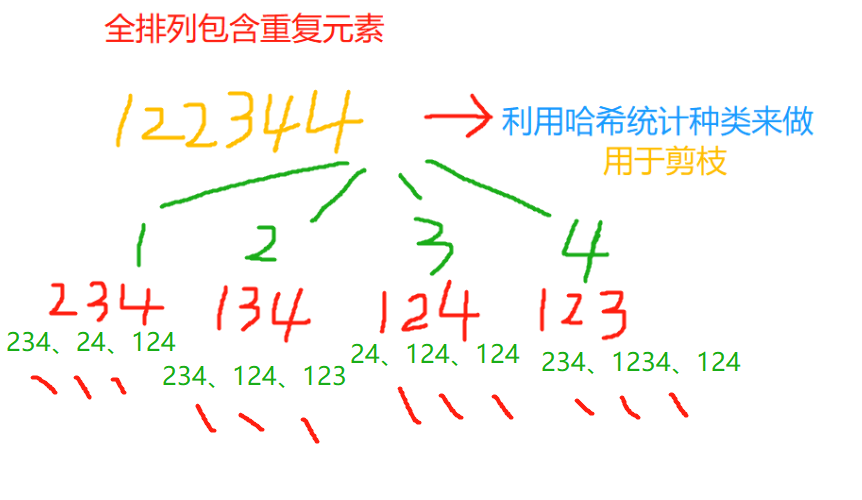
  • 解题：利用unordered_map来存储元素，从而避免重复元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
vector<vector<int>>res;
vector<vector<int>> permuteUnique(vector<int>& nums) {
	unordered_map<int, int>vis;
	int len = nums.size();
	for (auto it : nums)vis[it]++;

	vector<int>arr;
	dfs(vis, len, arr);
	return res;
}
void dfs(unordered_map<int, int>&vis, int len, vector<int>& arr) {
	//结束条件
	if (len == 0) {
		res.push_back(arr);
		return;
	}
	for (auto &it : vis) {
		//条件选择
		if (it.second == 0)
			continue;

		//做出选择
		it.second--;
		arr.push_back(it.first);

		//继续dfs
		dfs(vis, len - 1, arr);

		//撤销选择
		it.second++;
		arr.pop_back();
	}
}

———————————

组合问题———————

Just_123———————

39.组合中元素和为Sum（无重复元素、任意次数使用）

  • 给定一个无重复元素的数组 arr 和一个目标数 target ，找出 arr 中所有可以使数字和为 target 的组合。

  • arr 中的数字可以无限制重复被选取。

  • 输入：candidates = [2,3,6,7], target = 7,

  • 所求解集为：

  • [

  • [7],

  • [2,2,3]

  • ]

  • 解题：sort后：大剪枝

  • 可以重复使用：传入的还是index——传入一个开始的index，防止重复使用前面的元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
vector<vector<int>>res;
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
	vector<int>arr;
	//先排序
	sort(candidates.begin(), candidates.end());

	dfs(arr, candidates, target, 0);//0_index
	return res;
}

//这里的index很重要，防止重复223,232,322，又回去使用重复元素
void dfs(vector<int>&arr, vector<int>& candidates, int sum, int index) {
	if (sum == 0) {
		res.emplace_back(arr);
		return;
	}
	for (int i = index; i < candidates.size(); i++) {
		//条件选择
		if (sum - candidates[i] < 0)
			break;

		//做出选择(无限次用)
		arr.emplace_back(candidates[i]);
		//继续DFS
		dfs(arr, candidates, sum - candidates[i], i);
		//撤销选择
		arr.pop_back();
	}
}

40.组合中元素和为Sum II（重复元素、使用一次）

  • 给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

  • candidates 中的每个数字在每个组合中只能使用一次。

  • 题解：

    • sort后：大剪纸
    • 剔除重复的可能：小剪枝
      • if (i != index && candidates[i] == candidates[i - 1])
      • continue;
    • 元素只能使用一次传入index + 1

img1 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
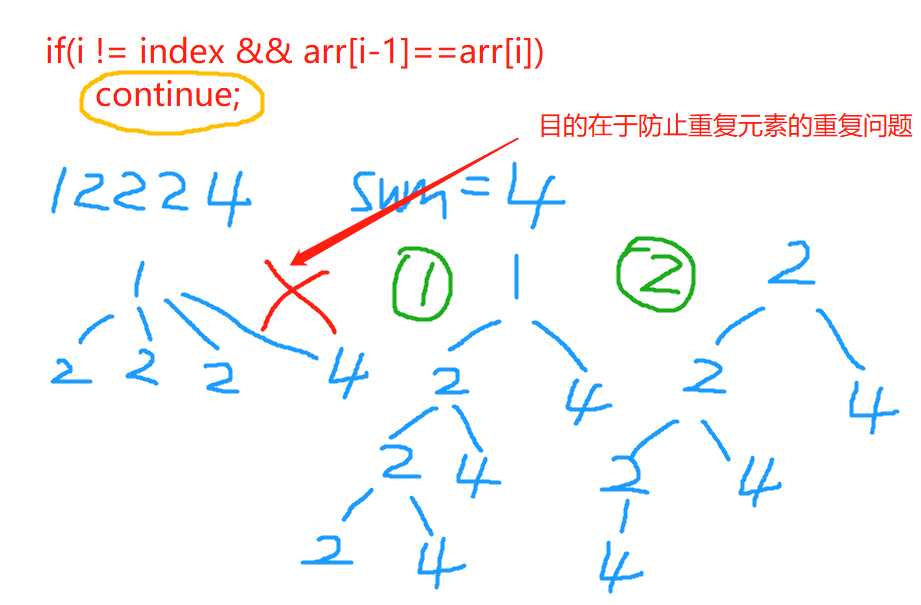
31
vector<vector<int>>res;
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
	vector<int>arr;
	sort(candidates.begin(), candidates.end());
	dfs(candidates, arr, target, 0);
	return res;
}
void dfs(vector<int>&candidates, vector<int>&arr, int target, int index) {
	if (target == 0) {
		res.emplace_back(arr);
		return;
	}
	for (int i = index; i < candidates.size(); i++) {
		//大剪枝
		if (target - candidates[i] < 0)
			break;
		//小剪枝：
		if (i != index && candidates[i] == candidates[i - 1])
			continue;

		//做出选择
		arr.emplace_back(candidates[i]);

		//继续dfs,index+1是因为不能重复使用元素
		dfs(candidates, arr, target - candidates[i], i + 1);

		//撤销选择
		arr.pop_back();

	}
}

78.数组内元素组成不同子集(不含重复元素)

  • 给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

  • 说明：解集不能包含重复的子集。

  • 输入: nums = [1,2,3]

  • 输出:

  • [

  • [3],

  • [1],

  • [2],

  • [1,2,3],

  • [1,3],

  • [2,3],

  • [1,2],

  • []

  • ]

  • 题解：sort后传入index辅助判断

    • 传入index+1：只能用一次 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
vector<vector<int>>res;
vector<vector<int>> subsets(vector<int>& nums) {
	vector<int>arr;
	dfs(nums, arr, 0);
	return res;
}
void dfs(vector<int>&nums, vector<int>&arr, int index) {
	//满足条件，加入res
	res.emplace_back(arr);

	for (int i = index; i < nums.size(); i++) {

		arr.emplace_back(nums[i]);

		dfs(nums, arr, i + 1);

		arr.pop_back();
	}
}

90.数组内元素组成不同子集II(包含重复元素)

  • 给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

  • 说明：解集不能包含重复的子集。

  • 输入: [1,2,2]

  • 输出:

  • [

  • [2],

  • [1],

  • [1,2,2],

  • [2,2],

  • [1,2],

  • []

  • ]

  • 题解：包含重复元素，只能用一次

  • 小剪枝：

  • if (i != index && candidates[i] == candidates[i - 1])

  • continue;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
vector<vector<int>>res;
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
	vector<int>arr;
	sort(nums.begin(), nums.end());
	dfs(nums, arr, 0);
	return res;
}
void dfs(vector<int>& nums, vector<int>& arr, int index) {
	res.emplace_back(arr);

	for (int i = index; i < nums.size(); i++) {
		if (i != index && nums[i] == nums[i - 1])
			continue;

		arr.emplace_back(nums[i]);
		dfs(nums, arr, i + 1);
		arr.pop_back();
	}
}

———————————

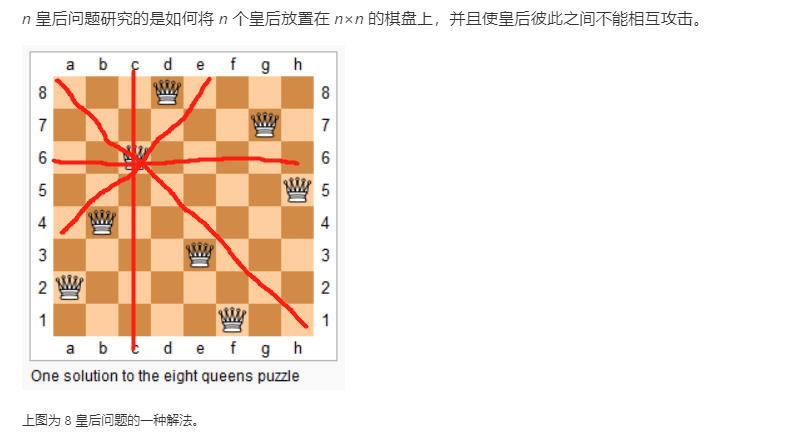
51.N皇后

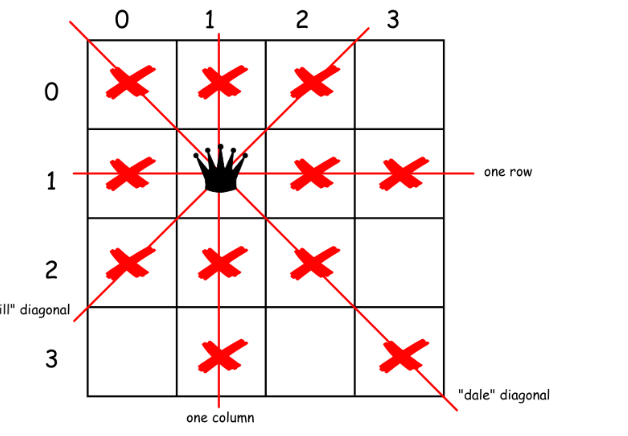
  • n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
    img
    img

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    vector<vector<string>>res;
    vector<vector<string>> solveNQueens(int n) {
    	//'.'表示空，'Q'表示皇后
    	//初始化棋盘，n行，n列
    	vector<string>board(n, string(n, '.'));
    	//0表示row = 0
    	backtrack(board, 0);
    	return res;
    }
    void backtrack(vector<string>&board, int row) {
    	if (row == board.size()) {
    		res.emplace_back(board);
    		return;
    	}
    	for (int col = 0; col < board[0].size(); col++) {
    		//排序不合法
    		if (!isValid(board, row, col)) continue;
    		//做选择
    		board[row][col] = 'Q';

    		backtrack(board, row + 1);
    		//撤销选择
    		board[row][col] = '.';
    	}
    }
    bool isValid(vector<string>&board, int row, int col) {
    	int n = board.size();
    	//检查列
    	for (int i = 0; i < n; i++) {
    		if (board[i][col] == 'Q')
    			return false;
    	}
    	//检查左上
    	for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; j--, i--) {
    		if (board[i][j] == 'Q')
    			return false;
    	}
    	//检查右上
    	for (int i = row - 1, j = col + 1; i >= 0 && j < n; j++, i--) {
    		if (board[i][j] == 'Q')
    			return false;
    	}
    	return true;
    }

93.复原IP地址的问题

  • 给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

  • 有效的 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 ‘.’ 分隔。

  • 例如：”0.1.2.201” 和 “192.168.1.1” 是 有效的 IP 地址，但是 “0.011.255.245”、”192.168.1.312” 和 “192.168@1.1“ 是 无效的 IP 地址。

  • 输入：s = “25525511135”

  • 输出：[“255.255.11.135”,”255.255.111.35”]

  • 输入：s = “0000”

  • 输出：[“0.0.0.0”]

img

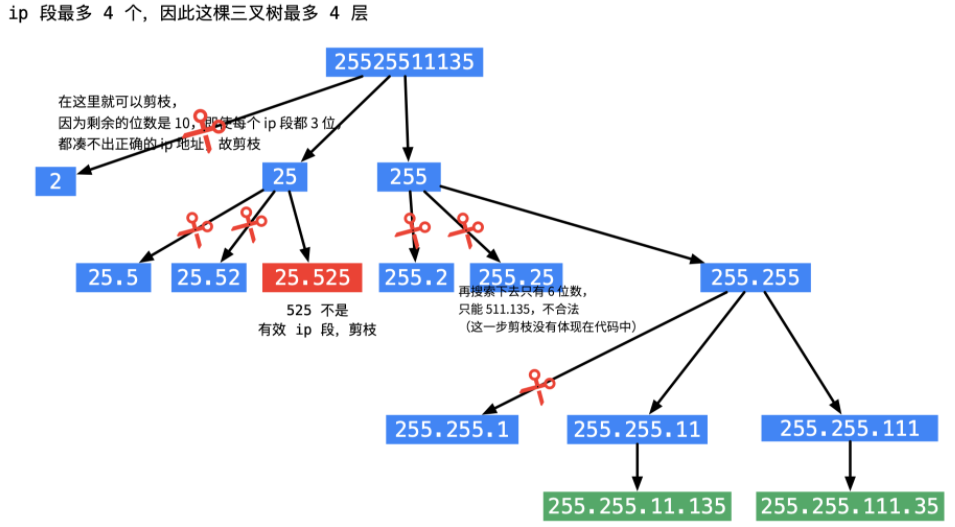
  • 解：不用考虑剩余元素的个数，只要直接最后判断：1.是否剩余元素 2.是否cnt=4

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
vector<string> restoreIpAddresses(string s) {
	vector<string>res;
	dfs(s, "", 0, res);
	return res;
}
void dfs(string s, string out, int cnt, vector<string>& res) {
	if (cnt == 4 && s.size() == 0) {
		out.pop_back();
		res.push_back(out);
		return;
	}
	if (cnt == 4 && s.size())
		return;

	for (int i = 1; i <= s.size() && i <= 3; i++) {
		string temp = s.substr(0, i);
		int num = stoi(temp);

		//防止出现0开头的数。01.01.01.01
		if (to_string(num).size() != temp.size())
			return;

		if (num >= 0 && num <= 255) {
			string before = out;
			//做出选择
			out += temp + ".";
			//继续dfs
			dfs(s.substr(i), out, cnt + 1, res);
			//撤销选择
			out = before;
		}
	}
}

22.括号的生成

  • 数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
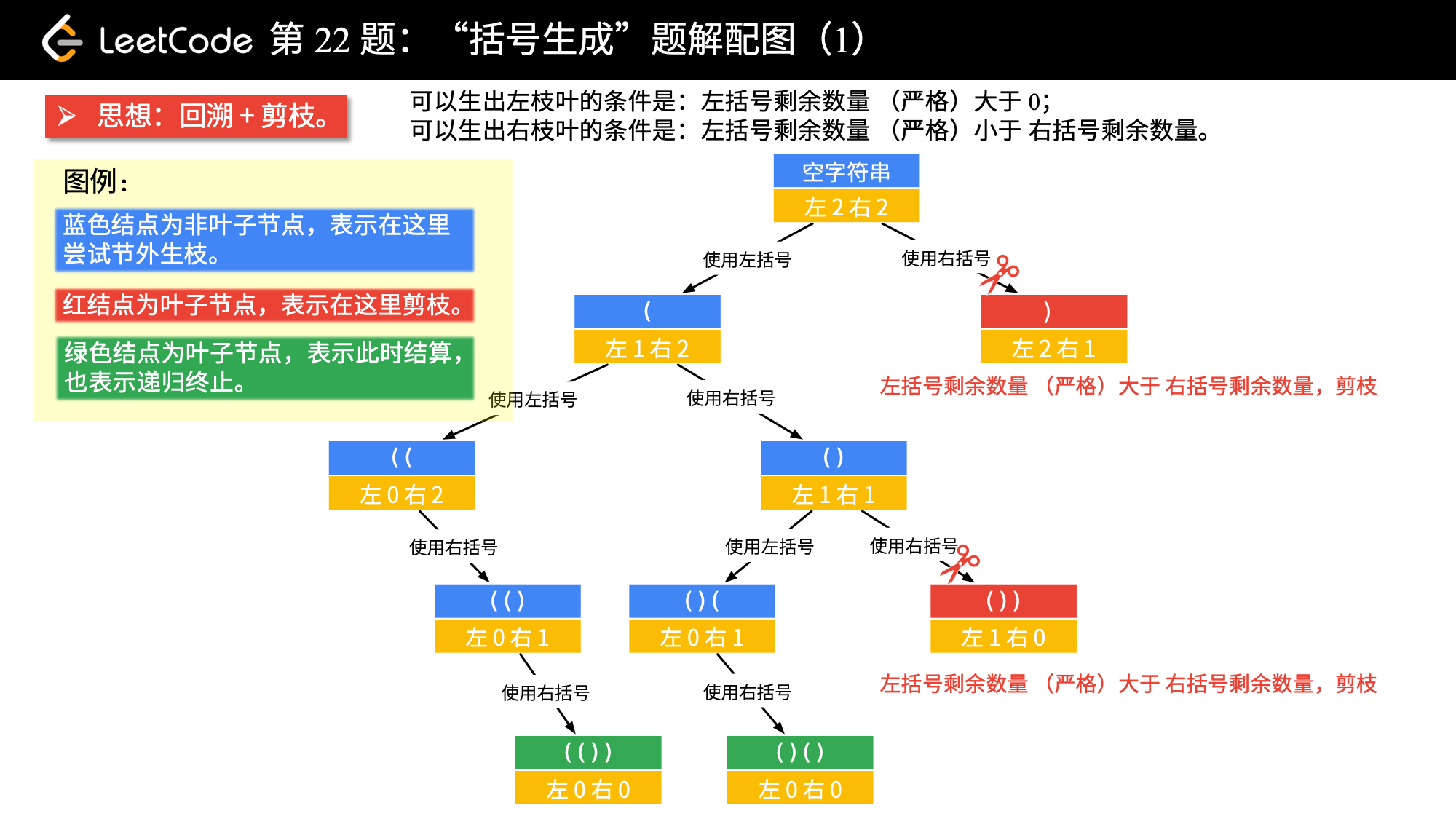
//回溯法dfs深度遍历
vector<string> generateParenthesis(int n) {
	if (n == 0)
		return { "" };
	vector<string>res;
	dfs(res, "", n, n);
	return res;
}
void dfs(vector<string>&res, string tmp, int L, int R) {
	if (L == 0 && R == 0)
		res.push_back(tmp);

	if (L > 0)
		dfs(res, tmp + '(', L - 1, R);
	if (R > 0 && R > L)
		dfs(res, tmp + ')', L, R - 1);

}
文章作者: Inter
文章链接: https://zuizichuan.cn/2020/08/18/LeetCode-%E5%9B%9E%E6%BA%AF%E6%B3%95/
版权声明: 本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Zichuan365' Blog！