bfs广度搜索
关键在于寻找种子
auto [tempX , tempY] = arr.front();
找到污染源
找到污染源
找到污染源
542. 01 矩阵
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1 。
输入:
0 0 0
0 1 0
0 0 0
输出:
0 0 0
0 1 0
0 0 0
输入:
0 0 0
0 1 0
1 1 1
输出:
0 0 0
0 1 0
1 2 1
解题:找到污染源,用0去污染1,距离就是污染源的值+1。queue所以能保证,路径先是1.然后是2。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> res(m, vector<int>(n, 0));
queue<pair<int, int>> q;
//找到为0的种子,入队列,0相当于烂橘子,污染源
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (matrix[i][j] == 0) {
q.push(make_pair(i, j));
}
}
}
int dx[4] = { 0,0,1,-1 };
int dy[4] = { 1,-1,0,0 };
while (!q.empty()) {
auto[i, j] = q.front();
q.pop();
for (int d = 0; d < 4; ++d) {
int ni = i + dx[d];
int nj = j + dy[d];
if (ni >= 0 && ni < m && nj >= 0 && nj < n && matrix[ni][nj] == 1)
{
//这部最重要
res[ni][nj] = res[i][j] + 1;
q.push(make_pair(ni, nj));
matrix[ni][nj] = 0;
}
}
}
return res;
}
994.烂橘子
在给定的网格中,每个单元格可以有以下三个值之一:
- 值 0 代表空单元格;
- 值 1 代表新鲜橘子;
- 值 2 代表腐烂的橘子。
- 每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
- 返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回-1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38int orangesRotting(vector<vector<int>>& grid)
{
int n = grid.size();
int m = grid[0].size();
int orangeNum = 0;
queue<pair<int, int>>Q;
//将污染源入队列
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (grid[i][j] == 2)
Q.push(make_pair(i, j));
int xDir[4] = { 0,0,1,-1 };
int yDir[4] = { 1,-1,0,0 };
while (!Q.empty()) {
int num = Q.size(); //现存的烂橘子数量
for (int i = 0; i < num; i++)
{
auto[X, Y] = Q.front();
Q.pop();
for (int j = 0; j < 4; j++) {
int x1 = X + xDir[j];
int y1 = Y + yDir[j];
if (x1 >= 0 && x1 < n && y1 >= 0 && y1 < m && grid[x1][y1] == 1) {
grid[x1][y1] = 2;
Q.push(make_pair(x1, y1));
}
}
}
//污染第一次循环结束,当还有橘子在队列说明此次又有好橘子被污染
if (!Q.empty())
orangeNum++;
}
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
if (grid[i][j] == 1)
return -1;
return orangeNum;
}
1162.地图分析
你现在手里有一份大小为 N x N 的 网格 grid,上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,请你找出一个海洋单元格,这个海洋单元格到离它最近的陆地单元格的距离是最大的。
我们这里说的距离是「曼哈顿距离」( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。
如果网格上只有陆地或者海洋,请返回 -1。

1 | int maxDistance(vector<vector<int>>& grid) |
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
- 给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
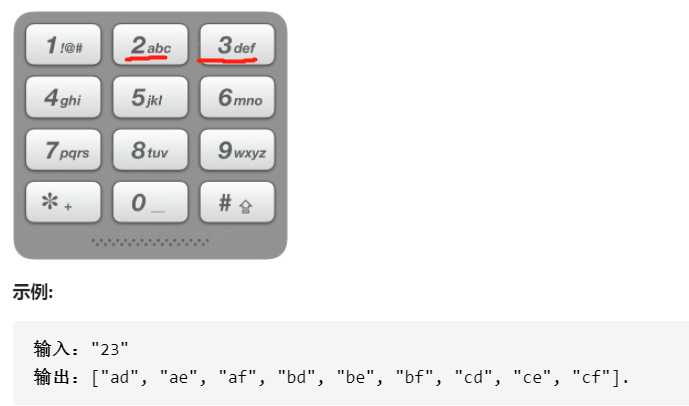
解:
- 1.利用map将数字和string对应关系确定。
- 2.然后利用queue依次遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30vector<string> letterCombinations(string digits) {
vector<string> res;
unordered_map<char, string> m = { {'2',"abc" },{'3',"def"},{'4',"ghi"},{'5',"jkl"},{'6',"mno"},
{'7',"pqrs"},{'8',"tuv"},{'9',"wxyz"} };
int size = digits.size();//输入字符串产长度
queue<string> que;//新建队列
//先将第一个元素对应的码表入队
for (int j = 0; j < m[digits[0]].size(); j++) {
string str;
str.push_back(m[digits[0]][j]);
que.push(str);
}
string s; //用于存储队头元素
for (int i = 1; i < size; i++) {
int length = que.size(); //当前队列长度
while (length--) {
for (int j = 0; j < m[digits[i]].size(); j++) {
s = que.front();
s = s + m[digits[i]][j];//队头元素加上新元素
que.push(s);//入队
}
que.pop();//队头出队
}
}
while (!que.empty()) {
res.push_back(que.front());
que.pop();
}
return res;
}
1030. 距离顺序排列矩阵单元格
给出 R 行 C 列的矩阵,其中的单元格的整数坐标为 (r, c),满足 0 <= r < R 且 0 <= c < C。
- 另外,我们在该矩阵中给出了一个坐标为 (r0, c0) 的单元格。
- 返回矩阵中的所有单元格的坐标,并按到 (r0, c0) 的距离从最小到最大的顺序排,其中,两单元格(r1, c1) 和 (r2, c2) 之间的距离是曼哈顿距离,|r1 - r2| + |c1 - c2|。(你可以按任何满足此条件的顺序返回答案。)
输入:R = 1, C = 2, r0 = 0, c0 = 0
输出:[[0,0],[0,1]]
解释:从 (r0, c0) 到其他单元格的距离为:[0,1]
输入:R = 2, C = 2, r0 = 0, c0 = 1
输出:[[0,1],[0,0],[1,1],[1,0]]
解释:从 (r0, c0) 到其他单元格的距离为:[0,1,1,2]
[[0,1],[1,1],[0,0],[1,0]] 也会被视作正确答案。
典型的广度搜索,起始节点为种子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {
vector<vector<int>>res;
vector<vector<bool>>vis(R, vector<bool>(C, true));
queue<pair<int, int>>arr;
arr.push({ r0,c0 });
vis[r0][c0] = false;
int dX[4] = { 0,0,1,-1 };
int dY[4] = { 1,-1,0,0 };
while (!arr.empty()) {
auto[x, y] = arr.front();
arr.pop();
res.push_back({ x,y });
for (int i = 0; i < 4; i++) {
int tempX = x + dX[i];
int tempY = y + dY[i];
if (tempX >= 0 && tempX < R && tempY >= 0 && tempY < C && vis[tempX][tempY]) {
vis[tempX][tempY] = false;
arr.push({ tempX,tempY });
}
}
}
return res;
}
