dfs深度搜索

找到递归关系
找到递归关系
找到递归关系

---

695.岛屿最大面积

• 给定一个包含了一些 0 和 1 的非空二维数组 grid 。

• 一个 岛屿 是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直方向上相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。
  

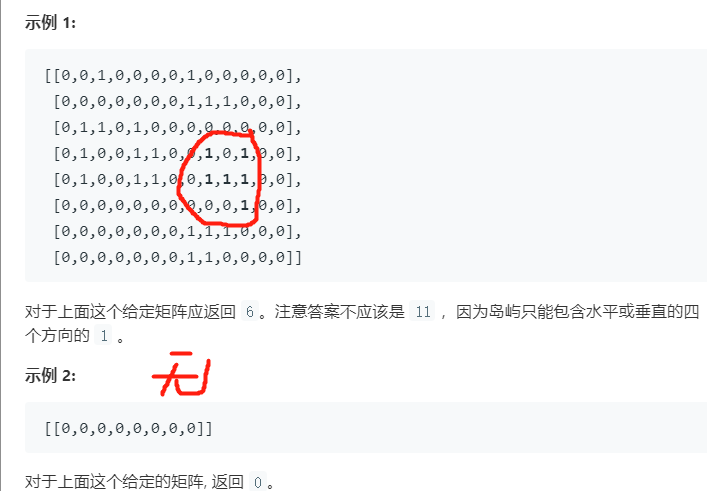
• 解题：因为一片联通区域一次性肯定是算出来了,就可以将访问过的路径置为0

  int dfsArea(vector<vector<int>>&grid, int i, int j) {
  	//界定范围，当是岛屿时，继续向外拓展，标定为0已经搜寻
  	//所以是引用操作，一片连着的岛屿只会搜寻一次整片区域
  	if (i < 0 || i == grid.size() || j < 0 || j == grid[0].size() || grid[i][j] == 0)
  		return 0;
  
  	grid[i][j] = 0;
  	int xDir[4] = { 0,0,1,-1 };
  	int yDir[4] = { 1,-1,0,0 };
  	//这此区域已经为陆地满足初始为1
  	int res = 1;
  	for (int m = 0; m != 4; m++) {
  		res += dfsArea(grid, i + xDir[m], j + yDir[m]);
  	}
  	return res;
  }
  
  int maxAreaOfIsland(vector<vector<int>>& grid) {
  	if (grid.size() == 0 || grid[0].size() == 0)
  		return 0;
  	int area = 0;
  	int maxArea = 0;
  	int n = grid[0].size();
  	for (int i = 0; i != grid.size(); i++) {
  		for (int j = 0; j != n; j++) {
  			if (grid[i][j] == 1) {
  				area = dfsArea(grid, i, j);
  				maxArea = max(maxArea, area);
  			}
  		}
  	}
  	return maxArea;
  }

---

剑指Offer12.矩阵中的路径(和695区别:需要回溯)

• 请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始，每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格，那么该路径不能再次进入该格子。例如，在下面的3×4的矩阵中包含一条字符串“bfce”的路径（路径中的字母用加粗标出）

• [[“a”,“b”,”c”,”e”],
• [“s”,“f”,“c”,”s”],
• [“a”,”d”,“e”,”e”]]

bool exist(vector<vector<char>>& board, string word) {
	int len = board.size();
	if (len == 0 || board[0].size() == 0 || word.empty())return false;
	vector<vector<bool>>vis(len, vector<bool>(board[0].size(), true));//辅助数组
	for (int i = 0; i < board.size(); i++) {
		for (int j = 0; j < board[0].size(); j++) {
			if (board[i][j] == word[0]) {
				if (dfs(i, j, board, word, 0, vis))
					return true;
			}
		}
	}
	return false;
}
bool dfs(int i, int j, vector<vector<char>>& board, string word, int length, vector<vector<bool>>&vis) {
	//回溯的返回条件
	if (length == word.size())
		return true;
	//排除不合法
	if (i < 0 || i >= board.size() || j < 0 || j >= board[0].size()
		|| vis[i][j] == false || board[i][j] != word[length])
		return false;

	//做出选择
	vis[i][j] = false;

	//回溯函数，有真则真
	bool res = dfs(i, j + 1, board, word, length + 1, vis) || dfs(i, j - 1, board, word, length + 1, vis) ||
		dfs(i + 1, j, board, word, length + 1, vis) || dfs(i - 1, j, board, word, length + 1, vis);

	//撤销选择
	vis[i][j] = true;
	return res;
}

---

0828笔试题—目标路径到目的路径

• 从（x1，y1）到（X，Y）路径上的最小和，同时遇到-1为路障，无法通过

• 输入：

• 3,4

• 1,3,4,-1

• -1,11,6,8

• -1,2,1,9

• 起始：(0，0)——>（2，1）

• 输出：16

int res = INT_MAX;
void dfs(vector<vector<int>>arr, vector<vector<bool>>&vis,int sum,int x,int y,int m,int n) {
	if (x < 0 || x >= arr.size() || y < 0 || y >= arr[0].size() || vis[x][y] == false)
		return;
	
	if (x == m && y == n) {
		res = min(res, sum);
		//cout << res << endl;
		return;
	}
	vis[x][y] = false;
	
	int XX[4] = { 0,0,1,-1 };
	int YY[4] = { 1,-1,0,0 };

	for (int i = 0; i < 4; i++)
		dfs(arr, vis, sum + arr[x][y], x + XX[i], y + YY[i], m, n);

	vis[x][y] = true;
}

---

329.矩阵中的最长递增路径

• 给定一个整数矩阵，找出最长递增路径的长度。

• 对于每个单元格，你可以往上，下，左，右四个方向移动。 你不能在对角线方向上移动或移动到边界外（即不允许环绕）。

• 输入: nums =

• [

• [9,9,4],

• [6,6,8],

• [2,1,1]

• ]

• 输出: 4

• 解释: 最长递增路径为 [1, 2, 6, 9]。

//暴力
int resres;
int m;
int n;
int longestIncreasingPath(vector<vector<int>>& matrix) {
	m = matrix.size();
	n = matrix[0].size();
	if (m == 0 || n == 0)
		return 0;
	vector<vector<bool>>vis(m, vector<bool>(n, true));
	int res = 0;
	for (int i = 0; i < m; i++) {
		for (int j = 0; j < n; j++) {
			resres = 0;
			dfs(i, j, matrix, vis, matrix[i][j] - 1,0);
			res = max(res, resres);
		}
	}
	return res;
}
void dfs(int i, int j, vector<vector<int>> matrix, vector<vector<bool>>& vis, int NUM,int cnt) {
	if (i < 0 || i >= m || j < 0 || j >= n || vis[i][j] == false || matrix[i][j] <= NUM) {
		resres = max(cnt, resres);
		return;
	}
	vis[i][j] = false;

	int tmp= matrix[i][j];
	int XX[4] = { 0,0,1,-1 };
	int YY[4] = { 1,-1,0,0 };
	for (int ii = 0; ii < 4; ii++) {
		dfs(i + XX[ii], j + YY[ii], matrix, vis, tmp, cnt+1);
	}

	vis[i][j] = true;
}

---

//优化版本:采用记忆法

int dfs(vector<vector<int>>& vis, vector<vector<int>>& matrix, int i, int j) {
	if (vis[i][j] != 0)
		return vis[i][j];

	vis[i][j] = 1;
	int cur = matrix[i][j];
	if (i - 1 >= 0 && matrix[i - 1][j] > cur)
		vis[i][j] = max(vis[i][j], dfs(vis, matrix, i - 1, j) + 1);
	if (i + 1 < matrix.size() && matrix[i + 1][j] > cur)
		vis[i][j] = max(vis[i][j], dfs(vis, matrix, i + 1, j) + 1);
	if (j - 1 >= 0 && matrix[i][j - 1] > cur)
		vis[i][j] = max(vis[i][j], dfs(vis, matrix, i, j - 1) + 1);
	if (j + 1 < matrix[0].size() && matrix[i][j + 1] > cur)
		vis[i][j] = max(vis[i][j], dfs(vis, matrix, i, j + 1) + 1);

	return vis[i][j];
}
int longestIncreasingPath(vector<vector<int>>& matrix) {
	if (matrix.size() == 0)
		return 0;
	int n = matrix.size();
	int m = matrix[0].size();

	int res = 0;
	vector<vector<int>>vis(n, vector<int>(m, 0));
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			res = max(res, dfs(vis, matrix, i, j));
		}
	}
	return res;
}