图像处理
1.图像概念
- 图像:是一个二维亮度函数,表示在空间XY坐标下,单点的亮度或灰度值。
- 二维亮度函数:f(x,y) = C
- 数字图像:是图像的数字化表示。数字图像是由许多个单点的单个元素所组成的,单个元素完美称为像素。
- 每个像素都有一个特定的位置和像素值。
2.图像颜色分类
- 单色(灰度)图
- RGB彩色图像
- RGB555:一种16位的RGB格式,最后一位不用
- RGB565:使用16位表示一个像素,这16位中的5位用于R,6位用于G,5位用于B。
- RGB24:正常的RGB表示方法
- RGB32:使用32位来表示一个像素,RGB使用24位,剩余8位_Alpha通道(透明度)或者不用。
- CMY和CMYK:RGB对立面
- C=255 - R
- M=255 - G
- Y=255 - B
- HSI:色调、饱和度、亮度
- YUV:一种颜色编码方式。常使用在各个视频处理组件中。 YUV在对照片或视频编码时,考虑到人类的感知能力,允许降低色度的带宽。
- Y:明亮度、U:色度、V:饱和度
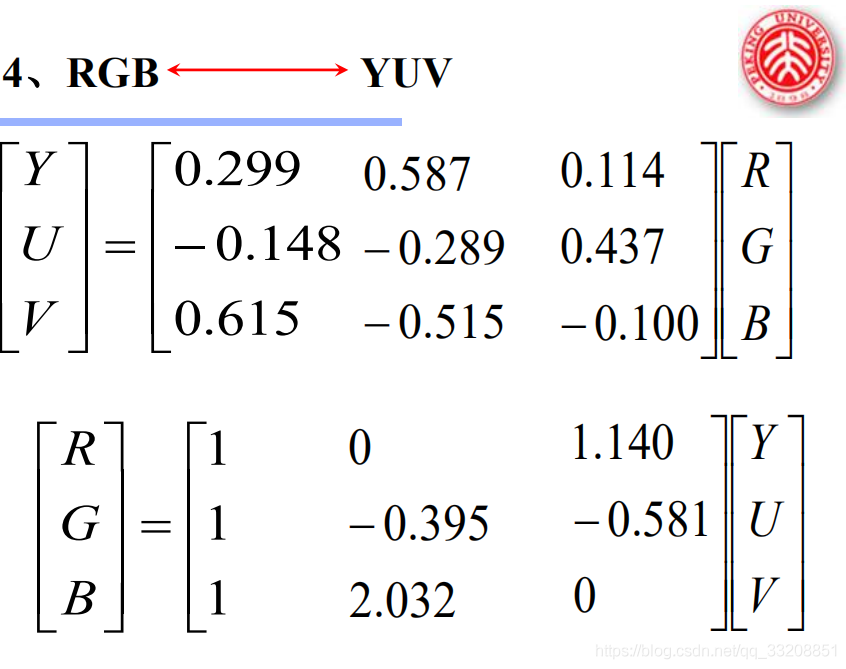
- Y:明亮度、U:色度、V:饱和度
3.像素间的关系
- p的4邻域:4个垂直和水平方向上的像素
- N_4(p)
- p的D邻域:4个对角邻域像素
- N_D(p)
- p的8邻域
- N_8(p)
4.图像的内容
- 颜色特征:直方图
- 纹理特征
- 形状特征
5.图像的傅里叶变换
定义:傅里叶变换是一种在空间域和频率域的变换。
- 空间域——>频率域:傅里叶变换
- 频率域——>空间域:傅里叶反变换
频域(frequency domain)
是指在对函数或信号进行分析时,分析其和频率有关部份,而不是和时间有关的部份,和时域一词相对。
时域
是描述数学函数或物理信号对时间的关系。例如一个信号的时域波形可以表达信号随着时间的变化。若考虑离散时间,时域中的函数或信号,在各个离散时间点的数值均为已知。若考虑连续时间,则函数或信号在任意时间的数值均为已知。在研究时域的信号时,常会用示波器将信号转换为其时域的波形。
两者相互间的变换
时域(信号对时间的函数)和频域(信号对频率的函数)的变换在数学上是通过积分变换实现。对周期信号可以直接使用傅立叶变换,对非周期信号则要进行周期扩展,使用拉普拉斯变换。
简单来说:频率越大的地方原始信号速度变化越快,频率越小的地方原始信号速度变化越慢。所以,在图像处理中,频域反映了图像在空域部分灰度的变化剧烈程度。
傅里叶变换提供了一条从空域到频率自由转换的途径。
重要概念:
图像高频分量:图像突变部分;在某些情况下指图像边缘信息,某些情况 下指噪声,更多是两者的混合;
低频分量:图像变化平缓的部分,也就是图像轮廓信息
高通滤波器:让图像使低频分量抑制,高频分量通过
低通滤波器:与高通相反,让图像使高频分量抑制,低频分量通过
带通滤波器:使图像在某一部分 的频率信息通过,其他过低或过高都抑制
还有个带阻滤波器,是带通的反。
